Поляризация света

Следствием теории Максвелла является поперечность световых волн: напряженность электрического поля E, вектор индукции магнитного поля B и скорость распространения волны v образуют правую тройку векторов. Действие света на вещество определяется в основном колебаниями вектора напряженности. В соответствии с этим вектор напряженности называют еще световым вектором.

Рассмотрим два взаимно перпендикулярные электрические колебания (вдоль осей x и y), отличающиеся по фазе на d

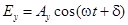, . (1)
Результирующая напряженность E является их векторной суммой. Угол j между вектором E и осью x определяется выражением

. (2)

Естественный свет. Поляризованным называется свет, в котором направления колебаний светового вектора упорядочены каким-либо образом. В естественном свете колебания различных направлений быстро и беспорядочно сменяют друг друга. Если разность фаз d претерпевает случайные хаотические изменения, то и угол j, т.е. направление светового вектора E, будет испытывать скачкообразные изменения. На этом основании естественный свет можно представить как наложение двух некогерентных световых волн, поляризованных во взаимно перпендикулярных плоскостях и имеющих одинаковую интенсивность.

Плоско поляризованный свет. Допустим, что разность фаз d постоянна и равна нулю или p (когерентные волны). Тогда согласно (2)

.
Следовательно, результирующее колебание совершается в фиксированном направлении. – волна оказывается плоско поляризованной.

Круговая и эллиптическая поляризация света. Допустим теперь, что . С учетом с помощью уравнения (1) можно получить

.
Следовательно, световой вектор в некоторой точке описывает при прохождении волны эллипс, оси которого ориентированы вдоль x и y. Такая волна называется эллиптически поляризованной. При произвольном постоянном d в общем случае получается эллиптическая поляризация, причем оси эллипса не совпадают с осями координат.

При разности фаз равной нулю или p, эллипс вырождается в прямую и получается плоско поляризованный свет. При и равенстве амплитуд складываемых волн эллипс вырождается в окружность – получается циркулярно поляризованный (поляризованный по кругу) свет.

В зависимости от направления вращения вектора E различают правую и левую эллиптическую и круговую поляризацию. Будем наблюдать за вращением вектора E со стороны, в которую движется волна. Если его вращение происходит по часовой стрелке, поляризация называется правой, в противном случае – левой.

Плоскость, в которой лежит световой вектор в плоско поляризованной волне, называется плоскостью колебаний. По историческим причинам плоскостью поляризации называется плоскость, перпендикулярная в плоскости колебаний, т.е. плоскость в которой лежит вектор B.

Плоско поляризованный свет можно получить из естественного с помощью приборов, называемых поляризаторами. Поляризаторы свободно пропускают колебания, параллельные некоторой плоскости (плоскости поляризатора), и полностью или частично задерживают колебания перпендикулярные этой плоскости. На выходе из поляризатора получается свет, в котором колебания одного направления преобладают над колебаниями другого. Такой свет называется частично поляризованным. Частично поляризованный свет, как и естественный, можно представить в виде наложения двух некогерентных плоско поляризованных волн с взаимно перпендикулярными плоскостями колебаний. В случае естественного света интенсивность этих волн одинакова, а в случае частично поляризованного – разная.

Если пропустить частично поляризованный свет через идеальный поляризатор, то при его вращении вокруг направления луча интенсивность прошедшего света будет изменяться в пределах от до . Выражение

(3)
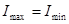называется степенью поляризации. Для плоско поляризованного света и ; для естественного света и 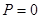. К эллиптически и циркулярно поляризованному свету, колебания которых полностью упорядочены, понятие степени поляризации не применимо, поскольку формальное применение (3) дает .

Пусть на идеальный поляризатор падает плоско поляризованный свет амплитуды A и интенсивности Исходное колебание можно разложить на два взаимно перпендикулярных колебания с амплитудами и , где j – угол между плоскостью поляризатора и плоскостью колебаний падающего света. Первое колебание пройдет через поляризатор, второе будет задержано. Интенсивность прошедшего света пропорциональна , т.е. равна

. (4)
Соотношение (4) носит название закона Малюса.

Поставим на пути естественного света два поляризатора, плоскости которых образуют угол j. Из первого поляризатора выйдет плоско поляризованный свет, интенсивность которого составляет половину интенсивности естественного света . После прохождения через два поляризатора интенсивность света будет равна

.
Максимальная интенсивность света () получается при j = 0 (поляризаторы параллельны). При скрещенных поляризаторах интенсивность равна нулю (свет не проходит).

Пусть эллиптически поляризованный свет падает на поляризатор. Он пропустит составляющую вектора E, параллельную плоскости поляризатора (рис.). Амплитуда и интенсивность плоско поляризованного на выходе света зависит от ориентации поляризатора. Она максимальна при совпадении плоскости поляризатора с большой полуосью эллипса и минимальна при совпадении первой с малой полуосью эллипса. Такой же характер изменения интенсивности света при вращении поляризатора получается в случае частично поляризованного света. В случае циркулярно поляризованного света вращение поляризатора не сопровождается, как и в случае естественного света, изменением интенсивности прошедшего света.

Поляризация света при отражении и преломлении. Закон Брюстера. Если угол падения на границу раздела двух диэлектриков (например, воздуха и стекла) отличен от нуля, отраженный и преломленный луч оказываются частично поляризо­ванными. В отраженном свете преобладают колебания, перпендикулярные к плоскости падения, в преломленном луче – колебания параллельные плоскости падения (рис.).

Степень поляризации отраженного и преломленного лучей можно получить с помощью формул Френеля. Эти формулы выводятся из граничных условий для электромагнитного поля на границе раздела двух диэлектриков. Каждую (падающую, отраженную, преломленную) световую волну можно представить в виде суперпозиции двух волн, колебания в одной из которых совершаются в плоскости падения, а в другой – перпендикулярно этой плоскости. В обозначениях

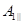и – амплитуды падающих волн,

и – амплитуды отраженных волн,

и – амплитуды преломленных волн,
формулы Френеля имеет следующий вид

, , (5)

, , (6)
Из этих формул вытекает, что преломление происходит при всех условиях без изменения фазы волны. При отражении происходит изменение фазы, зависящее от следующих условий. При падении под углом, меньшим угла Брюстера (см. ниже), отражение от оптически более плотной среды сопровождается изменением фазы на p; отражение от оптически менее плотной среды происходит без изменения фазы. В случае, когда 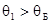, фазовые соотношения для обеих компонент оказываются различными.

Обозначим через угол падения, при котором (отраженный и преломленный лучи взаимно перпендикулярны). Из первой формулы получается, что при падении под углом амплитуда обращается в нуль. Следовательно, в отраженной волне присутствуют лишь колебания, перпендикулярные к плоскости падения, – отраженная волна полностью поляризована. Из закона преломления несложно установить, что

. (7)
Это соотношение носит название закона Брюстера, а угол называют углом Брюстера.

С помощью формул Френеля можно определить интенсивности отраженного и преломленного света. Для малых углов падения в результате получается

, .

Поляризация при двойном лучепреломлении. При прохождении света через все прозрачные кристаллы, за исключением кристаллов, принадлежащих к кубической системе, наблюдается явление, получившее название двойного лучепреломления. Это явление заключается в том, что упавший на кристалл луч разделяется внутри кристалла на два луча, распространяющиеся, вообще говоря, с разными скоростями и в разных направлениях.

Кристаллы, обладающие двойным лучепреломлением, подразделяются на одноосные и двуосные. У одноосных кристаллов имеется одно направление, вдоль которого лучи распространяются, не разделяясь, с одинаковой скоростью. Это направление называются оптической осью кристалла. У двухосных кристаллов имеются два таких направления (две оптические оси).

У одноосных кристаллов (исландский шпат, кварц, турмалин) один из преломленных лучей подчиняется обычному закону преломления. Этот луч называется обыкновенным и обозначается буквой o. Другой луч называется необыкновенным и обозначается буквой e. Преломление необыкновенного луча происходит по другому закону. Даже при нормальном падении света на кристалл необыкновенный луч, вообще говоря, отклоняется от нормали. Кроме того, необыкновенный луч не лежит, как правило, в одной плоскости с падающим лучом и нормалью к преломляющей поверхности. У двухосных кристаллов (слюда, гипс) оба луча необыкновенные. В дальнейшем речь будет идти только об одноосных кристаллах.

Исследования показывают, что вышедшие из кристалла лучи плоско поляризованы во взаимно перпендикулярных плоскостях. Плоскость, проходящая через луч света и оптическую ось кристалла, называется главной плоскостью (или главным сечением) кристалла. Колебания светового вектора в обыкновенном луче происходят перпендикулярно главной плоскости, в необыкновенном – в главной плоскости (рис.).

Двойное лучепреломление объясняется анизотропией кристаллов. В кристаллах некубической системы диэлектрическая проницаемость e зависит от направления. В одноосных кристаллах e в направлении оптической оси и в направлениях, перпендикулярных к ней, имеет различные значения и . В других направлениях e имеет промежуточное значение. Показатель преломления 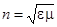. Для большинства прозрачных веществ практически m = 1, поэтому можно считать .

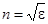В обыкновенном луче световой вектор перпендикулярен оптической оси кристалла и, следовательно, скорость распространения луча для всех направлений будет одна и та же . Расстояние от точечного источника света до волновой поверхности пропорциональна лучевой скорости в соответствующем направлении. Поэтому, если в кристалле находится такой источник, то волновая поверхность для обыкновенных лучей является сферой.

В необыкновенном луче световой вектор лежит в главной плоскости. Для луча, распространяющегося вдоль оптической оси, световой вектор перпендикулярен оптической оси. Скорость распространения луча в этом направлении такая же как для обыкновенного . Для луча, распространяющегося перпендикулярно оси, . Для других лучей скорость имеет промежуточное значение. Можно показать, что волновая поверхность необыкновенных лучей представляет собой эллипсоид вращения. В местах пересечения с оптической осью волновой эллипсоид необыкновенного луча и волновая сфера обыкновенного соприкасаются.

Одноосные кристаллы характеризуются показателем преломления обыкновенного луча и показателем преломления необыкновенного луча . В зависимости от того, какая из скоростей, или , больше, различают положительные и отрицательные одноосные кристаллы (рис.). У положительных кристаллов (или ). У отрицательных кристаллов (или ).

Ход обыкновенного и необыкновенного лучей в кристалле можно определить с помощью принципа Гюйгенса. При построении, нужно учитывать, что лучами являются линии, вдоль которых распространяется энергия световой волны. Как будет видно ниже, нормаль к волновой поверхности не обязательно совпадает с направлением луча.

На рис. изображены три случая нормального падения света на поверхность кристалла, отличающиеся направлением оптической оси. В случае а лучи o и e распространяются вдоль оптической оси не разделяясь. В случае б оптическая ось кристалла параллельна преломляющей поверхности. При нормальном падении света обыкновенный и необыкновенный лучи идут в одном направлении, но с разной скоростью. В случае в обыкновенный луч o после преломления распространяется вдоль нормали к поверхности кристалла. Необыкновенный же луч e заметно отклоняется от нормали.

Анализ поляризованного света. Пусть на кристаллическую пластинку, вырезанную параллельно оптической оси, нормально падает плоско поляризованный свет (рис.). Внутри пластинки он делится на обыкновенный и необыкновенный лучи, которые в кристалле движутся в одном направлении с разными скоростями. На входе в пластинку разность фаз d этих лучей равна нулю, на выходе из пластинки

.
Вырезанная параллельно оптической оси пластинка, для которой

,
называется пластинкой в четверть волны. При прохождении через такую пластинку обыкновенный и необыкновенный лучи приобретают разность фаз ±p/2.

Плоско поляризованный свет, можно представить как суперпозицию двух волн, поляризованных вдоль оптической оси кристалла и перпендикулярного ей направления (т.е. обыкновенного и необыкновенного луча) с разностью фаз, равной нулю. Пластинка, при прохождении этих лучей, внесет разность фаз ±p/2. Следовательно, плоско поляризованный свет превращается в эллиптически поляризованный (в частном случае в циркулярно поляризованный). Параметры поляризации определяются разностью фаз d и углом между плоскостью поляризации исходной волны и оптической осью кристалла.

Эллиптически поляризованный свет можно представить как суперпозицию двух волн, поляризованных вдоль главных полуосей эллипса, с разностью фаз ±p/2 (в случае циркулярно поляризованного света в виде волн, поляризованных вдоль любых двух взаимно перпендикулярных направлений). Если на пути эллиптически поляризованного света поместить пластинку в четверть волны, оптическая ось которой ориентирована параллельно одной из осей эллипса (в случае циркулярно поляризованного ориентация пластинки произвольна), то она внесет дополнительную разность фаз ±p/2. Результирующая разность фаз станет равной нулю или p.

Циркулярно поляризованный свет, пройдя пластинку, становится плоско поляризованным. Если на пути луча поставить поляризатор, то можно добиться полного его гашения. Если же падающий свет естественный, то он при прохождении пластинки таковым и останется (при любом положении пластинки и поляризатора интенсивность прошедшего поляризатор луча не меняется).

Эллиптически поляризованный свет, пройдя соответствующим образом ориентированную пластинку (ее оптическая ось совпадает по направлению с одной из осей эллипса), превращается в плоско поляризованный. Прошедший свет можно погасить поворотом поляризатора. При произвольной ориентации пластинки на выходе получится эллиптическая поляризация, но с другими параметрами.

Таким образом, с помощью пластинки в четверть волны и поляризатора можно отличить эллиптически поляризованный свет от частично поляризованного или циркулярно поляризованный свет от естественного.

Искусственное двойное лучепреломление. В прозрачных аморфных телах, а также кристаллах кубической системы может возникать двойное лучепреломление под влиянием внешних воздействий. Первоначально оптически изотропные вещества становятся оптически анизотропными под действием: 1) одностороннего сжатия или растяжения (кристаллы кубической системы, стекла); 2) электрического поля – эффект Керра (жидкости, аморфные тела, газы); 3) магнитного поля – явление Коттон-Мутона (жидкости, стекла). Вещество при указанных воздействиях приобретает свойства одноосного кристалла, оптическая ось которого совпадает с направлением деформации, электрического или магнитного полей соответственно.

Возникающая при воздействии оптическая анизотропия характеризуется разностью показателей преломления обыкновенного и необыкновенного лучей (для последнего в направлении перпендикулярном оптической оси)

(в случае деформации);

(в случае электрического поля);

(в случае магнитного поля),
где , , 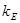– постоянные, характеризующие вещество, s – нормальное напряжение, E и H – соответственно напряженность электрического и магнитного полей.

Двойное лучепреломление при деформации связано с деформационной анизотропией первоначально изотропного кристалла. Эффект Керра (как и явление Коттон-Мутона) объясняется различной поляризуемостью молекул по разным направлениям. Под действием электрического поля молекулы, обладающие дипольным моментом, приобретают преимущественную ориентацию по полю. Аналогичная ситуация возникает в магнитном поле, если молекулы вещества обладают собственным магнитным моментом.

Поиск по сайту: