 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Симплекстік-кесте
Кесте
| x | F(x)=2.1 sin0.37x |
| -3.2 | -1.9449 |
| -0.6126 | |
| 0.4 | 0.3097 |
| 2.8 | 1.8068 |
| 4.0 | 2.0913 |
| 6.4 | 1.4673 |
| 7.6 | 0.6797 |
| x | F(x)=1/x*lg x+x2 |
| 1.3 | 1.7777 |
| 2.1 | 4.5634 |
| 3.7 | 13.8436 |
| 4.5 | 20.3952 |
| 6.1 | 37.3387 |
| 7.7 | 59.4051 |
| 8.5 | 72.3593 |
4.14-кесте
4.12-кесте
| x | 
|
| 2.6 | 2.1874 |
| 3.3 | 2.8637 |
| 4.7 | 3.8161 |
| 6.1 | 3.8524 |
| 7.5 | 3.1905 |
| 8.2 | 2.8409 |
| 9.6 | 2.6137 |
Кесте
| x | F(x)=ln 2.3x-0.8/x |
| 1.2 | 0.3486 |
| 1.9 | 1.0537 |
| 3.3 | 1.7844 |
| 4.7 | 2.2103 |
| 5.4 | 2.3712 |
| 6.8 | 2.6322 |
| 7.5 | 2.7411 |
4.13-кесте 4.15-кесте
4.16-кесте
| Вариант номері | 2 тапсырма | 3 тапсырма | ||||
| кесте | х | кесте | a | b | h | |
| 4.6 | 3.8 | 4.11 | 0.65 | 0.75 | 0.025 | |
| 4.7 | 3.5 | 4.12 | 0.30 | 0.45 | 0.01 | |
| 4.8 | 0.5 | 4.13 | 1.45 | 1.55 | 0.02 | |
| 4.9 | 4.8 | 4.14 | 1.20 | 1.40 | 0.01 | |
| 4.6 | 4.1 | 4.12 | 0.10 | 0.20 | 0.02 | |
| 4.7 | 3.9 | 4.13 | 1.10 | 1.30 | 0.025 | |
| 4.8 | 3.3 | 4.14 | 1.05 | 1.25 | 0.02 | |
| 4.9 | 4.11 | 0.70 | 0.90 | 0.025 | ||
| 4.6 | 2.9 | 4.13 | 1.25 | 1.50 | 0.01 | |
| 4.7 | 5.3 | 4.14 | 1.10 | 0.01 | ||
| 4.8 | 4.1 | 4.11 | 0.60 | 0.70 | 0.01 | |
| 4.9 | 7.6 | 4.12 | 0.15 | 0.35 | 0.025 | |
| 4.6 | 4.4 | 4.14 | 1.15 | 1.25 | 0.01 | |
| 4.7 | 2.5 | 4.11 | 0.65 | 0.85 | 0.025 | |
| 4.8 | 5.2 | 4.12 | 0.20 | 0.40 | 0.02 | |
| 4.9 | 6.8 | 4.13 | 1.15 | 1.25 | 0.01 |
4.19-кесте 4.18 кесте
4.17-кесте
| x | Sin x |
| 1.10 | 0.89121 |
| 1.15 | 0.91276 |
| 1.20 | 0.93204 |
| 1.25 | 0.94898 |
| 1.30 | 0.96356 |
| 1.35 | 0.97572 |
| 1.40 | 0.98545 |
| 1.45 | 0.99271 |
| 1.50 | 0.99749 |
| 1.55 | 0.99973 |
| 1.60 | 0.99957 |
| x | Cos x |
| 0.05 | 0.99375 |
| 0.10 | 0.99500 |
| 0.15 | 0.99877 |
| 0.20 | 0.98007 |
| 0.25 | 0.96891 |
| 0.30 | 0.95534 |
| 0.35 | 0.93937 |
| 0.40 | 0.92106 |
| 0.45 | 0.90045 |
| 0.50 | 0.87758 |
| 0.55 | 0.85252 |
| x | sin x |
| 0.60 | 0.56464 |
| 0.65 | 0.60519 |
| 0.70 | 0.64422 |
| 0.75 | 0.68164 |
| 0.80 | 0.71736 |
| 0.85 | 0.75128 |
| 0.90 | 0.78333 |
| 0.95 | 0.81342 |
| 1.00 | 0.84147 |
| 1.05 | 0.86742 |
| 1.10 | 0.89121 |
Зертханалық жұмыс №10-11
Тақырыбы: Сызықтық дифференциалдау және интегралдау.
1 -Тапсырма: Лагранждың немесе Ньютонның интерполяцияланған формулаларын қолдана отырыпдаблицалық түрде берілген функция туындысының
мәнін калькулятордың көмегімен есептеңіз және бүл әдістің қателігін бағалаңыз.
2 -Тапсырма: Аналитикалық түрде берілген f(х) функцияның
функцияның туындысының бір мәнін есептеу үшін программасын
құрып, оны ЭЕМ-де есептеңіздер.
3 - Тапсырма: Берілген f(х) функциясының интегралын [а,Ь] кесіндісін теңдей 10 бөлікке бөле отырып, трапеция және Симпсон әдісінің формулалары бойынша калькулятордың көмегімен есептеңіздер. Интегралдау әдісінің қателігін бағалап,алынған нәтиженің дәлдігін салыстыру керек. Бөлінген аралықтың қайсысында дәлдік Е=10"6 дәлдігі орындалатынын
анықтаңыздар.
4-Тапсырма: Симпсон формуласы бойынша [а,Ъ] кесіндісінде берілген функция интегралының мәнін есептеу үшін, программасын күрып, ЭЕМ-де Е=10-6 дәлдігімен есептеңіз.
5-ші Зертханалық жүмысты орыңдау барысы, 1-ші тапсырманы орындау үшін 4.17- 4.20 кестелерінің негізгі берілгендері қолданылады, олар "3_ Тапсырма" бөлімінің 4.16 кестесіндегі вариант номерінің сәйкес келуімен таңдалынады.Дифференциалдау үшін кестенің бөлігі, х аргументтің мөні,сонымен бірге қолданатын әдісті мүғалім өзі береді.
2-ші тапсырма да, 1-ші тапсырманы орындау үшін қодданылатын мәліметтермен орындалады, тек мүндағы айырмашылық, бұл 4.17-4.20 кестелерінен функция мәндерінің кестелік емес, аналитикалық өрнегі алынады.Туындының табылған мәнін, 1-ші тапсырманы орындағандағы табылған мәнмен, сонымен қатар формула бойынша тікелей дифференциалдаудан кейінгі берілген функцияның туындысын есептегендегі нәтижемен салыстырамыз.
3-ші тапсырманы орындау үшін негізгі мәліметтерді 5.5 кестеден аламыз. Интегралдау кесіндісі бірдей 10 тең бөлікке бөлінеді және Симпсон, трапеция формулалары бойынша интегралды есептеу жүргізіледі. Бүл мақсатта интеграл астындағы функция мәңдерінің біртүтас кестесін схема бойынша құрастыру ыңғайлы:
Кесте
| Xi | Yi/2(i=0.10) | Yi (i=1,2,3,…,9) | 2yi (i=1,3,5,7,9) |
Кестенің үш бағанасының әрқайсысында, интеграл астындағы функцияның сәйкес мәндерінің қосындысы орналасқан. Есептеулер максимал дәлдікпен жүргізіледі. 4-ші тапсырманы орындамастан бұрын 5.10 параграфты жақсылап оқып жаттап есептің қайталану әдісінің бар болуын жақсылап талдау керек.
Бұл тапсырманы орындау үшін қажетті мәліметтерді 5.7 кестеден алуға болады.
Кесте
| Варианттар | F(x) | A | B |
| 0.37esin x | |||
| 0.5x+xlg x | |||
| (x+1.9)sin(x/3) | |||
| 1/x ln(x+2) | |||
| 3 cosx/2x+1.7 | |||
| (2x+0.6) cos(x/2) | |||
| 2.6x2 lnx | 1.2 | 2.2 | |
| (x2+1)sin(x-0.5) | 0.5 | 1.5 | |
| x2 cos(x/4) | |||
| sin(0.2x-3)/x2+1 | |||
| 3x+ln x | |||
| 4xex2 | -1 | ||
| 3x2+tg x | -0.5 | 0.5 | |
| 3x2+sin x/x2 | |||
| 3xecos x | 0.2 | 1.2 | |
| x2tg x/2 | 1.5 | 2.5 |
Зертханалық жұмыс № 12-13
Тақырыбы: Бірінші ретті қарапайым дифференциалдық теңдеулерді сандық шешу.
Тапсырма: У'=f(х,у) дифференциалдық теңдеуі үшін [ а;в ] кесіндісінде берілген бастапқы шарттарын У(а) = с және интегралдау адымын h деп қабылдап, Коши есебін шығар:
1) Эйлер әдісімен адымды 2h —де және адымдап h деп ЭВМ —да (МК-да
алынған кесте бойынша интегралдық қисық графигінің көрінісін сал);
2) Рунге-Кутта әдісімен адымдап 2h және h деп ЭВМ- да;
3) Кітапханалық бағдарламаны қолдану арқылы.
Тапсырманың нүсқаға арналған бастапқы деректері 6.1 кестесінде берілген.
6.1- кесте
| Вариант | a | b | c | h | |
| xy3-x2 | 0.7 | 0.1 | |||

| 2.6 | 4.6 | 1.8 | 0.2 | |
| cos(1,5x-y2)-1,3 | -1 | 0.2 | 0.2 | ||
| X2+xy-y2 | 1.2 | 0.2 | |||
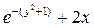
| 0.5 | 0.3 | 0.05 | ||
| cos(1,5y-x)2-1,4 | 0.9 | 0.1 | |||
| 4,1x-y2+0.6 | 0.6 | 2.6 | 3.4 | 0.2 | |
  
| 1.5 | 2.1 | 0.05 | ||
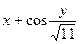
| 2.1 | 3.1 | 2.5 | 0.1 | |

| 1.7 | 0.2 | |||
| 2,5-cos(y+0,6) | 1.5 | 0.2 | |||
| x+2.5y2+2 | 0.9 | 0.1 | |||
| 2-sin(x+y)2 | 2.3 | 0.1 | |||
 
| 0.1 | 0.5 | 1.25 | 0.05 | |

| -2 | -1 | 0.1 | ||

| 2.9 | 0.2 | |||
| sin(x+e)+1,5 | 1.5 | 2.5 | 0.5 | 0.1 |
Зертханалық жұмыс № 14-15
Тақырыбы: Тәжірибелік мәліметтердің статистикалық өңделуі
Тапсырма: Берілген кесте бойынша У белгісінің нәтижелік мәні және факториалдық белгінің берілуін (мысалы, х1) неғүрлым кіші квадраттар әдісімен екі әртүрлі эмпирикалық формаларды және алынған жуықтаудың сапасын қүрамыз.
Зертханалық жұмысты орындауға түсінік.
7.1 -7.3 материалын оқып және 7.3.1 мысалын қарастыру. Берілген кесте бойынша нүктелік график құрылады, оның көмегімен неғұрлым жуықтау функциясы таңдалады. Мұнда жақындаудың ең жақын түрін табудың қандай да бір жалпы әдісін көрсету мүмкін емес, көп жағдайда осы есепті сәтті шешу зерттеушінің тәжірибесі мен сезіміне тәуелді. ЭЕМ-ды пайдалану кезінде көп күш жұмсамай-ақ әртүрлі әдістерді сынақтан өткізу мүмкіндігі пайдаланылады ОХ пен ОУ остерінде масштабтарды дұрыс қиюластыру және координаталар жүйесінде графикті дұрыс орналастыру нүктелік графикті зерттеу мен жуықтау функциясын таңдауды жеңілдетеді. Эмприкалық формуланы құру кезінде аргументтің алғашқы мәндері және функциялар оң болуына қол жеткізуге болатынын байқауға болады.
Бұл үшін остердің бағытына қарай параллелді тасымалдау жеткілікті, яғни жаңа айнымалыға өтуге болады, сонымен бірге, соңғы нәтиже жазбасында алғашқы белгілеулерге қайту қажет.
Жуықтау функциясының түрін таңдағаннан кейін есептерге кірісу қажет. Егер есептеу калькулятор көмегімен берілсе, онда көмекші кестені қолдану ыңғайлы (кесте 7.4, 7.5). ЭЕМ-ді пайдалануда берілген түрдегі жуықтау функцияларының параметрлер мәнінің қорытындысы және оларға сәйкес келетін квадраттарының программасы құрылады.
Кейбір жағдайларда эмприкалық формуланы жақсартуға қол жеткізуге болады. Қарапайым өдіс келесідей болады, ү = F(х) табылған эмприкалық
функция болсын, ал оған сәйкестенетін квадраттар ауытқуы  (7.8 формуланы қарастырамыз).
(7.8 формуланы қарастырамыз). 
 функциясын қарастырамыз, мүндағы С- соші. Егер
функциясын қарастырамыз, мүндағы С- соші. Егер  қабылдасақ,
қабылдасақ,  формуласы
формуласы 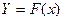 формуласына қарағанда квадраттық ауытқу қосындысын ең аз мәніне сәйкестелетінін [6] көрсету қиын емес. Сонымен С мәні 0-ге қарағанда көбірек ерекшеленеді.
формуласына қарағанда квадраттық ауытқу қосындысын ең аз мәніне сәйкестелетінін [6] көрсету қиын емес. Сонымен С мәні 0-ге қарағанда көбірек ерекшеленеді.
Алғашқы мәліметтермен жұмыс 7.7 кестеде орналасқан. 1. Тапсырманың 1- бөлімі калькуляторда немесе ЭВМ-да орындалады. (6.3.1 есепті қарандар). Қол және машинкамен есептелген жауаптарды бір кестеге толтыру.
Функцияның мәні өзінің жолдарымен бір-бірімен салыстырмалы түрде құрастырылады, ал дәл жауабы. Микрокалькуляторде есептегенде функцияның графигі салынады, қисық шығады. Тапсырманың екінші бөлімінде ЭВМ-нің программасы құрастырылады, екі рет шығады-бірінші шыққанда  , екіншісінде
, екіншісінде  (сол бір интегралдық кесіндіде [а;в].
(сол бір интегралдық кесіндіде [а;в].
Салыстыра келе дәл нәтижесі шығады. Эйлердің тұжырымы бойынша. Егер  есептелгенде У(х) функциясы 2h-қа, h арқылы Уn-тің
есептелгенде У(х) функциясы 2h-қа, h арқылы Уn-тің
жуық мәндерін табуға болады. е табу үшін уһ мына формуланы пайдалану керек 
ОСӨЖ күнтізбелік-тақырыптық жоспары
| № | Сабақтың тақырыбы және мазмұны | Сағат саны | Апта | Өткізу формасы |
| 1. | Қателіктерді табу. Абсолюттік және салыстырмалы қателіктер. | Электронды нұсқа | ||
| 2. | Сызықты емес теңдеулерді шешу. Графикалық әдіс. Кесіндіні қақ бөлу әдісі. | Электронды нұсқа | ||
| 3. | Сызықты емес теңдеулерді шешу. Хорда (Қию) және Ньютон әдістері. Қателіктерді есептеу. | Электронды нұсқа | ||
| 4. | Сызықтық алгебралық теңдеулер жүйесін сандық әдістерімен шешу. Гаусс әдісі. | Электронды нұсқа | ||
| 5. | Сызықтық алгебралық теңдеулер жүйесін сандық әдістерімен шешу. Жәй итерация мен Зейдел әдістері. | 5-6 | Электронды нұсқа | |
| 6. | Сызықтық программалау есебін шешудің симплекстік әдісі. | 7-8 | Электронды нұсқа | |
| 7. | Функцияларды интерполяциялау. Лагранж және Ньютонның интерполияцияланған көпмүшелігі. | Электронды нұсқа | ||
| 8. | Сандық дифференциялау | Электронды нұсқа | ||
| Сандық интегралдау. | Электронды нұсқа | |||
| 9. | Бірінші ретті қарапайым дифференциалдық теңдеулер үшін Коши есебін сандық әдіспен шешу. | Электронды нұсқа | ||
| 10. | Тәжірибелік мәліметтердің статистикалық өңделуі. Гиперболалық, параболалық және Лаплас теңдеуі үшін Дирихле есебін тор әдісімен шешу. | 13-14 | Электронды нұсқа | |
| Дербес туыңдылары бар дифференциалды теңдеулерді шешудің сандық әдістері | Электронды нұсқа | |||
| Барлығы: |
СӨЖ-ның күнтізбелік-тақырыптық жоспары
| № | Тапсырмалардың мазмұны | Сағат саны | Тапсыру мезгілі | Бақылау түрі |
| 1. | Есептеу математикасы пәні. Қателіктер теориясының элементтері. | 4-апта | Жазбаша | |
| 2. | Сызықтық алгебралық теңдеулер жүйесін шешу. Бірнеше теңдеулер жүйесін шешу. | 7-апта | Жазбаша | |
| 3. | Функцияның жуықтауы жөніндегі теориясы. | 11-апта | Жазбаша | |
| 4. | Математикалық физика есептерін шешу. | 14-апта | Жазбаша | |
| Барлығы: |
СӨЖ мақсаты және оны орындауға әдістемелік ұсыныстар
Студенттің өзіндік жұмысының мақсаты – студенттіңөз бетіншебілім алу қабілетін қалыптастыру болып табылады.
Көздеген мақсатқа жету үшін алдымызға қойылатын міндеттер:
· студенттіңөз бетіншебілім алу қабілетін қалыптастыруда теориялық материалдарды өздігінше тапсырмаға байланысты іздеп табу;
· табылған материалдарға талдау жасай білу;
· оқулықтар мен ғылыми-әдістемелік әдебиеттермен жұмыс істеу дағдыларын меңгеру және т.б.
· Біздің курс бойынша өздік жұмысқа 52 сағат берілген.
Өңдеудің құрамында өздік жұмыстар үшін арналған 10 тақырып бар. Студенттер көрсетілген материалды өз бетінше түсініп алулары керек және жасалған жұмыс туралы арнайы бөлінген уақытта мұғалімге баян етулері керек. Сонымен қатар, барлық студенттер тақырыптарда көрсетілген сол бір теориялық материал бойынша жұмыс істейді, ал сәйкес мәселелерді шешуде нұсқалар (варианты) бойынша бөлінеді. Нұсқалар бойынша студенттердің бөлінуін оқытушы іске асырады. Әр тақырып сәйкес әдебиетпен қамтылған. Өздік жұмыстарды көрсетілген бақылау түріне сай орындау қажет.
Пән бойынша студенттерге берілетін тапсырмалардың тақырыптары төмендегіше түрде берілді:
1-тақырып. Есептеу математикасы пәні. Қателіктер теориясының элементтері.
Қарастырылатын мәселе:
1. Математикалық модельдеу және есептеу эксперименті. Сандық әдістерге қойылатын негізгі талаптар.
2. Есепті шешу қателіктерінің классификациясы. Тиімді, орнықты алгоритмдер. Қисымдылық. Жуықтау.
3. Функция қателікгі. Абсолютті және салыстырмалы қателіктер.
2-тақырып. Сызықтық алгебралық теңдеулер жүйесін шешу. Бірнеше теңдеулер жүйесін шешу.
Қарастырылатын мәселе:
1. Сызықтық алгебрадан қосымша мәліметтер. Матрица нормалары.
2. Үш диогональды матрицамен берілген сызықтық жүйені шешуге арналған қуу әдісі.
3. Квадрат түбір әдісі.
3-тақырып. Функцияның жуықтауы жөніндегі теориясы.
Қарастырылатын мәселе:
1. Есептің берілуі. Функцияларды интерполияциялау есебі.
2. Чебышев көпмүшелігі.
3. Эйткеннің есептеу схемасы.
4-тақырып. Математикалық физика есептерін шешудің сандық әдістері.
Қарастырылатын мәселе:
1. Аппроксимация айырымы. Жылу өткізгіштік және тербелістің бір өлшемді теңдеулері үшін айырымдық сұлбалар.
2. Айырымдық сұлбалар үшін максимум принципі.
3. Монотонды айырымдық сұлбалар. Екі қабатты айырымдық сұлбалардың орнықтылықты және жинақтылықты зерттеудегі айнымалыларды бөлу әдісі.Торлы шеттік есептерді шешудің итерациялық әдістері.
ГЛОССАРИЙ
Сандық әдістер – қолданбалы математика бойынша мамандарды жалпы математикалық сауаттылыққа дайындауда ең негізгі фундаментальдық пәндердің бірі. Бұл пән – дәл мәнін есептеу мүмкін емес болған жағдайда жуықтап есептеу арқылы есептердің шешімін табуға арналған жоғары математиканың өте маңызды тарауы.
Талдау - бүтінді құрамды бөліктерге жіктеп талдауға негізделген ғылыми-зерттеу әдісі.
Математикалық модельдеу – дегеніміз практикалық есептердің шешуі дұрыс берілген мәліметтерден және есептің мақсаты қатаң түрде алынған математикалық ұғым түрінде сипатталуы және оның шартының нақты тұжырымдамасының жасалуы.
Эксперимент – кез-келген теориялық негіздеменің іс-жүзінде сынақталып оның не оң немесе қанағаттандырмайтын шешімінің анықталуынберетін ұғым.
Алгоритм - біртіндеп орындалған кезде белгілі бір мәселені немесе мәселелерлдің белгілі бір тобына кіретін кез келген мәселені шешуге мүмкіндік беретін нұсқаулардың ретімен орындалуы.
Технология – өндіріс процестерінде шикізаттарды өңдеу тәсілдері мен өнімдерді дайындау жолдарының өзара байланысты жүйесі.
Графиктік тәсіл – кез-келген функцияның кескіндеме түрінде бейнеленуі.
Мақсаттық функция – сызықтық программалау есептерін шешу барысында қолданылатын мәні теріс элементтерден немесе нөлдерден тұратын функция атауы.
Сызықтық программалау – математикалық анализдің әдістері жарамсыз келетін, есептің ең үлкен және ең кіші мәндерін іздейтін есептеумен айналысатын математикалық бөлімі.
Минимум мән – зерттелетін функцияның ең кіші мәні.
Максимум мән – зерттелетін функцияның ең үлкен мәні.
Итерациялық әдіс - жай қаталау әдісі немесе жуықтап шешу деген түсінікті
Базистік айнымалылар – сызықтық программалау есептерін шешу үшінтабылатын айнымалылар тізбегі.
Интерполяция -жуықталған функцияның табылуы
Интерполяциялау түйіндері – жуықталған функцияның мәндерінің бір-біріне сәйкес келуі.
Аналитикалық тәсіл – есептердің жалпы формула түрінде берілуі.
Түбірді жекелеу – берілген функцияның шешімі жататын аралықты табу.
Дәрістер кешені
Дәріс №1. Кіріспе. “Сандық әдістер” курсы пәні оның мақсаты мен міндеттері. Қателіктер теориясы
Жоспар:
1. “Сандық әдістер” курсы пәні оның мақсаты мен міндеттері.
2. Қолданбалы есептерді шешу кезеңдері.
3. Есепті шешудегі қателіктердің классификациясы.
Кілттік сөздер: Сандық әдістер, математикалық модель, алгоритм, ЭЕМ.
1. “Сандық әдістер” курсы пәні оның мақсаты мен міндеттері.
“Сандық әдістер” пәні оның мақсаты мен міндеттері оның қажеттілігі, өзектілігі жөніндегі мәліметтер силлабустың бас жағында толығымен келтірілді.
Ғылым мен техниканың қарқындап дамуы және электрондық есептеу машиналарының (ЭЕМ) жоғары сапалы түрлерінің пайда болуы табиғаттағы зерттелетін құбылыстардың математикалық модельдері болып табылатын есептерді құрастыруды және оларды қойылған есептің шарттарына лайық етіп берілген дәлдікпен шеше білу мәселесін алға қойып отыр.
Сондықтан оларды әрбір ғылым саласына лайықты түрдегі мүмкіндіктеріне қарай пайдалана білу керек.
Қазіргі заманда ғылыми техникалық есептердің тиімді шешудің дәрежесі ЭЕМ-ді дұрыс қолдана білуге байланысты. Осы мақсат үшін қуатты және ыңғайлы жалпыға ортақ дербес үлкен және кіші электрондық машиналар ғана емес сонымен бірге сандық әдістерді есептеуге ыңғайлы жаңа өңделген құралдар баршылық.
Қалай болса да есептеу процесінің әрқайсысының өз қиындығы бар және соңғы нәтиженің ақиқаттығына ықпалын тигізетін бірнеше кезеңнен өтеді. Зертханалық есептердің шешуі дұрыс берілген мәліметтерден және есептің мақсаты қатаң түрде алынған математикалық ұғым түрінде сипатталуынан басталады. Шарттың нақты тұжырымымен шешудің мақсаты ол математикалық есептің қойылуы. Шешімнің бұл кезеңі м атематикалық модельдердің тұрғызылуы деп аталады.
2. Қолданбалы есептерді шешу кезеңдері.
ЭЕМ-ді қолдана отырып есептерді шешу жалпы жағдайда келесі кезеңді қамтиды:
· есептің берілуі;
· математикалық моделін құру;
· алгоритмдері өңдеп талдау;
· есептің алгоритмін жазу;
· программасын құру;
· ЭЕМ-де есептеп шығару;
· алынған нәтижені талдау.
Бұл кезеңдердің ішіндегі ең күрделісі және жауаптысы математикалық модельдерді құру болып табылады.
3. Есепті шешудегі қателіктердің классификациясы.
Есептеулер процесінде жуықталған сандармен жұмыс істеуге тура келеді. А-кейбір шаманың дәл мәні делік. Келешекте А санын дәл сан деп аталық. А шаманың жуықталған мәнін немесе жуықталған санын  делік, яғни А шаманың дәл мәнін ауыстыратын
делік, яғни А шаманың дәл мәнін ауыстыратын  санын жуықталған сан деп аталық.
санын жуықталған сан деп аталық.
Егер  <A болса, онда
<A болса, онда  санын А санының кемімен алынған жуықталған мәні деп атайды.
санын А санының кемімен алынған жуықталған мәні деп атайды.
Егер  >A болса, онда
>A болса, онда  санын А санының артығымен алынған жуықталған мәні деп атайды.
санын А санының артығымен алынған жуықталған мәні деп атайды.
Мысалы: 3,14 саны 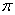 санының кемімен алынған жуықталған мәні болса, ал 3,15 сол
санының кемімен алынған жуықталған мәні болса, ал 3,15 сол 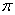 санының артығымен алынған жуықталған мәні болады. Осындай жақындаудың дәлдік дәрежесін сыйпаттау үшін "қателік” ұғымын пайдаланады.
санының артығымен алынған жуықталған мәні болады. Осындай жақындаудың дәлдік дәрежесін сыйпаттау үшін "қателік” ұғымын пайдаланады.
 (1.1)
(1.1)
айырымын жуықталған  санының кателігі деп атайды. Мұнда А-сәйкес дәл сан.
санының кателігі деп атайды. Мұнда А-сәйкес дәл сан.
Анықтама: Жуықталған  санның абсолюттік қателігі деп осы санның қателігінің абсолют шамасын айтады, яғни оны былай жазады:
санның абсолюттік қателігі деп осы санның қателігінің абсолют шамасын айтады, яғни оны былай жазады:
 (1.2)
(1.2)
Әдеттегідей дәл А саны белгісіз болатындықтан “шекті абсолют қателік” ұғымын пайдаланады.
Анықтама. Жуықталған  санының шекті абсолют қателігі деп осы
санының шекті абсолют қателігі деп осы  санының абсолют қателігінен аз болмайтын санды айтады, яғни
санының абсолют қателігінен аз болмайтын санды айтады, яғни
 (1.3) Ол сан бірмәнді анықталмайды: оны өсіруге болады. Сонда (1.3)-тен алатынымыз:
(1.3) Ол сан бірмәнді анықталмайды: оны өсіруге болады. Сонда (1.3)-тен алатынымыз:
 (1.4)
(1.4)
Демек,


 , (1.5)
, (1.5)
яғни  кемімен алған А санының жуықталған мәні, ал
кемімен алған А санының жуықталған мәні, ал  – А санының артығымен алынған жуық мәні. (1.5) формуланы қысқаша былай жазуға болады:
– А санының артығымен алынған жуық мәні. (1.5) формуланы қысқаша былай жазуға болады:  (1.6)
(1.6)
Практикада шаманың дәлдігін түсіну кезінде шекті абсолют қателігін пайдаланады. Мысалы, егер екі пунктің S=900 м тен арақашықтық 0,5 м дәлдікпен алынса, онда S шаманың дәл мәні
899,5 м < S < 900,5 м
шекаралықты алынатын болады.
Әдетте абсолют қателік (  ) екі-үш маңызды (значащие) таңбалы санмен жазады, ал маңызды таңбаларды санау кезінде сол жақтағы нольдер саналмайтынын естен шығармау керек. Мысалы: 0,004060 санында 4 маңызды таңба бар.
) екі-үш маңызды (значащие) таңбалы санмен жазады, ал маңызды таңбаларды санау кезінде сол жақтағы нольдер саналмайтынын естен шығармау керек. Мысалы: 0,004060 санында 4 маңызды таңба бар.
Мысалы: Қандайда бір есептеу машинасына тек 3 маңызды таңбалы сандарды ғана енгізу мүмкін болсын.  онда
онда 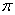 санын қандай дәлдікпен енгізуге болады. Шешімі:
санын қандай дәлдікпен енгізуге болады. Шешімі:  деп алуға болады.
деп алуға болады.
Жуықталған санның дәлдік дәрежесін сипаттау үшін абсолюттік немесе шекті абсолют қателік ұғымдары жеткіліксіз. Жуықталған сандардың дәлдігінің елеулі көрсеткіші олардың салыстырмалы қателігі.
Анықтама. Жуықталған  санының салыстырмалы қателігі деп осы санның абсолют қателігінің сәйкес дәл А санының модулына қатынасын айтады.
санының салыстырмалы қателігі деп осы санның абсолют қателігінің сәйкес дәл А санының модулына қатынасын айтады.
Оны былай белгілейді:
 (1.7)
(1.7)
Анықтама. Жуықталған  санының шекті салыстрмалы қателігі деп салыстырмалы қателіктен кем емес
санының шекті салыстрмалы қателігі деп салыстырмалы қателіктен кем емес  санын айтады, яғни
санын айтады, яғни
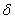

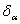 (1.8)
(1.8)
Егер (7) ескерсек, онда (8) келесі түрде жазуға болады:
 (1.9)
(1.9)
Демек, егер (1.3) пен (1.9) салыстырсақ, онда  санының шекті абсолют қателігі етіп келесі теңдікті жазуға болады:
санының шекті абсолют қателігі етіп келесі теңдікті жазуға болады:
 (2.10)
(2.10)
Егер  етіп қабылдасақ, онда (2.10) формуласын былай жазуға болады:
етіп қабылдасақ, онда (2.10) формуласын былай жазуға болады:
 (2.11)
(2.11)
Егер (2.11) теңдікті пайдалансақ, онда (2.5) теңсіздік келесі түрде түрленеді:

немесе
 (2.12)
(2.12)
Егер шекті салыстырмалы  қателік берілсе, онда (2.10) формула бойынша шекті абсолют
қателік берілсе, онда (2.10) формула бойынша шекті абсолют  қателікті анықтауға болады.
қателікті анықтауға болады.
Мысалы:  %
%
Жуық санның салыстырмалы қателігі ондағы дұрыс таңбалардың санымен байланысты, ал дұрыс таңбалардың саны (берілген) санның бірінші маңызды таңбасынан бастап оның абсолют қателігіндегі бірінші маңызды таңбаға дейінгі сандармен анықталады.
Дәріс №2. Бір белгісізі бар теңдеулерді шешудің сызықтық есебі. Түбірді жекелеу. Кесіндіні қақ бөлу
Жоспар:
1. Есептің берілуі.
2. Графиктік әдіспен түбірді жекелеу.
3. Аналитикалық әдіспен түбірді жекелеу.
4. Кесіндіні қақ бөлу әдісі
Кілттік сөздер: График, аналитикалық, механика, физика, жекеленген түбір
1. Есептің берілуі.
Бір белгісізі бар сызықты емес теңдеулерді шешу - қолданбалы математиканың, механиканың, физиканың және тағы да басқа аймақтардың әртүрлі бөлімдерінде туындайтын ең маңызды есептердің бірі болып табылады.
Сызықтық емес теңдеулерді жалпы жағдайда келесі түрде жазуға болады:
Ғ (х)=0 (1)
мұндағы, Ғ (х) функциясы [ а; b ] аралығында анықталған және үздіксіз. Кез-келген Ғ (х) функциясын 0-ге айналдыратын  кесіндісінде
кесіндісінде  саны табылып, сонда
саны табылып, сонда  = 0 болса, онда
= 0 болса, онда  нүктесі (1) теңдеудің түбірі деп аталады.
нүктесі (1) теңдеудің түбірі деп аталады.
Сандық әдістер пәнінде бір белгісізі бар теңдеулерді шешудің екі кезеңі бар:
1. Түбірлерді жекелеу;
2. Жекеленген түбірдің дәл мәнін белгілі бір әдіспен шешу.
1. Түбірді жекелеу дегеніміз - берілген теңдеудің түбірі жататын [a,b] кесіндісін анықтау. Теңдеудің түбірлерін табу - дегеніміз функцияның шеткі нүктелерін анықтау.Түбірді жекелеудің екі түрі бар:
2). Графиктік әдіс.
Берілген f(X) функциясының графигін сызамыз, сол аралықтан түбір жататын аралықты аламыз.
Егер f(х)- тің графигін салу күрделі болса немесе қиынға түссе, онда оны екі функция түрінде бөліп аламыз да, олардың жеке-жеке графиктерін саламыз. Содан соң олардың қиылысу нүктесін шешім ретінде қабылдаймыз (1-сурет).
Мысалы:

1-сурет. Күрделі функциядан түбір табу кескіні.
Көп жағдайда күрделі функциялардың шешімін табу үшін берілген F(x) функцияның мәнінің қай аралықта жатқандығын анықтау үшін графикалық тәсілді қолдану ыңғайлы. Бұл, көп жағдайда күрделі функцияларды шешу үшін қолданылады.
3) Аналитикалық әдіс.
Түбірді жекелеудің аналитикалық әдісі дегеніміз - формула түрінде берілген теңдеуді зерттеу арқылы түбір жатқан аралықты табу керек.
Аналитикалық әдісті зерттеу үшін: f(х)= 0 теңдеуі беріледі,[а,b]-аралығында
f(а)*f(b)< анықтау керек.
1. F(x) Функцияның 1- ші ретті туындысын f'(Х)- анықтау керек.
2. f'(Х)= 0 функциясының қауіпті нүктесін табу керек.
3. Осы қауіпті нүктесіндегі функцияның анықталу облысындағы таңбасын анықтау керек.
4. Функция таңбаларының кестесін анықтап олардың ара қашықтығын жиілету керек.
2. Жекеленген түбірдің дәл мәнін белгілі бір әдіспен шешу.
Атап айтатын болсақ: Бір белгісізі бар теңдеулерді шешудің сандық әдістеріне «кесіндіні қақ бөлу», «хорда», «жанама», «аралас» және «жай қайталау» әдістері жатады.
4) Дихотомия кесіндіні қақ бөлу әдісі.
1) Бізге f(х)=0 теңдеуі берілген.
2) f(х) - үздіксіз болсын.
3) ол екі рет туындалатын болсын, олар [а,b] - аралықтарында таңбаларын өзгертпесін. (1)-теңдеудің бір түбірі [а,b] аралықтарында жатсын.  яғни осы аралықтың шеткі нүктелерінде f(х)- әр түрлі мән қабылдасын (2-сурет).
яғни осы аралықтың шеткі нүктелерінде f(х)- әр түрлі мән қабылдасын (2-сурет).
f(а)*f(b)<0
Бізге (1)-ші тендеудің  -түбірін є-дәлдікпен анықтау керек.
-түбірін є-дәлдікпен анықтау керек.
Ол үшін берілген f(х)- функциясының шеткі нүктелерін алып, оны қақ бөлеміз.  1) Бізге керегі
1) Бізге керегі
f(а)*f(b)<0 шарт орындалу керек;
2) Үздіксіз болу қажет;
3) f(х), f(х)- таңбаларын өзгертпесін,
f(а)f(b)>0
Біздің шарт орындалмайды, демек бізге керегі жоқ, онда лақтырып тастаймыз. Енді [а1,b1]-аралығын қарастырайық:
f(а1)*f(b1)<0.

2-сурет. Дихотомия әдісінің жалпы көрінісі
Осылай жүргізген амалымызды бірнеше рет қайталаймыз, қателікті есептейтін келесі процесс орындалғанша:
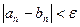 болғанша жалғастырамыз.
болғанша жалғастырамыз. 
f(аn)*f(bn)<0.
Демек, кесіндіні қақ бөлу әдісінің жалпы формуласы келесі түрде беріледі:

бірақ, кесіндіні қақ бөлу әдісінің формуласын қолдана отырып есептер шығару үшін, төмендегі шарт міндетті түрде орындалу керек:
 , мұндағы,
, мұндағы,  -ді 0-ге барынша жуықтағанша жалғастырамыз.
-ді 0-ге барынша жуықтағанша жалғастырамыз.
Дәріс №3. Бір белгісізі бар теңдеулерді шешудің Хорда әдісі және жанама әдісі.
Жоспар:
1. Бір белгісізі бар теңдеулерді шешудің кесіндіні хорда және жанама әдістері, олардың геометриялық мағынасы.
2. Хорда және жанама әдістерін қолдана отырып берілген есептердің бағдарламасын құру және оны ЭЕМ-де жүзеге асыру.
3. Қателіктерін бағалау.
Кілттік сөздер: Х орда, жанама, формула, қателік
1. Бізге F(x)=0 теңдеуі берілсін. Осы F(x)-функциясының x-осімен қиылысқан жерлеріндегі  түбірін табу керек, біздің графигімізде ол түбір А-арқылы көрсетілген.
түбірін табу керек, біздің графигімізде ол түбір А-арқылы көрсетілген.

3-сурет. Хорда әдісінің геометриялық кескіндеме түріндегі көрінісі.
Оны табу үшін функцияның шеткі нүктелері ММ* нүктелерін қосатын Хорда жүргіземіз. Осы хорданың х осімен қилысқан нүктесін D1 деп белгілейміз де осы нүктеден Хорданы қосатындай у осіне параллель түзу жүргіземіз. Оны M1 деп белгілейміз. Енді [M0, M*]- нүктелерінен өтетін түзудің теңдеуін жазамыз.
Формуламен сәйкестендіру сіздерге тапсырма ретінде беріледі. Жалпы түрде бір белгісізі бар теңдеулерді хорда әдісімен шешудің жолы 3-суретте келтірілді.
 мұндағы
мұндағы  бұдан
бұдан 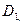 - ді табамыз. Сонда
- ді табамыз. Сонда

Енді 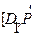 ]- нүктелерінен өтетін Хорданың теңдеуін жазамыз.
]- нүктелерінен өтетін Хорданың теңдеуін жазамыз.

деп белгілеп алып,  -ні табамыз да осы процесті жалғастыра береміз.
-ні табамыз да осы процесті жалғастыра береміз.

Енді  тізбегінің шегін табамыз.
тізбегінің шегін табамыз.
 бұл Хорда әдісінің жалпы формуласы болып табылады. Бірақ, мұнда есептелінген
бұл Хорда әдісінің жалпы формуласы болып табылады. Бірақ, мұнда есептелінген  -нің мәнінің дәлдігін қалайша бағалау мәселесі шешілмей отыр.
-нің мәнінің дәлдігін қалайша бағалау мәселесі шешілмей отыр.
Бұл мәселені шешу үшін  айырмасына шектеулі өсімшелер формуласын қолданамыз:
айырмасына шектеулі өсімшелер формуласын қолданамыз:
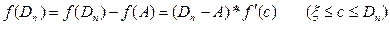

Мұнан
 егер де қарастырылып отырған аралықта (оны алдын ала біржолата есептеп қоюға болады)
егер де қарастырылып отырған аралықта (оны алдын ала біржолата есептеп қоюға болады)  -тің ең кіші мәнін m - мен белгілесек, онда былайша бағалауға болады:
-тің ең кіші мәнін m - мен белгілесек, онда былайша бағалауға болады:
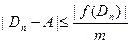
Сөйтіп,  шамасы бойынша да
шамасы бойынша да  -нің түбірге қаншалықты жақындығын айтуға болады екен.
-нің түбірге қаншалықты жақындығын айтуға болады екен.
2. Ньютон (жанама) әдісі
Бұл әдістің хордалар әдісінен айырмашылығы  -ншы итерацияда хорданың орнына
-ншы итерацияда хорданың орнына 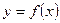 қиыстығына
қиыстығына  нүктелерінде жанама жүргізіледі, сонымен бірге Ғ (х)=0 (1) теңдеудің, түбірі орналасқан
нүктелерінде жанама жүргізіледі, сонымен бірге Ғ (х)=0 (1) теңдеудің, түбірі орналасқан  кесіндісін табу қажет емес, оның орнына түбірдің алғашқы жуықтауы болатын
кесіндісін табу қажет емес, оның орнына түбірдің алғашқы жуықтауы болатын  санын алу жеткілікті.
санын алу жеткілікті.
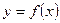 функциясына координаталары
функциясына координаталары  және
және  болатын
болатын  нүктелерінде жүргізілген жанаманың теңдеуі
нүктелерінде жүргізілген жанаманың теңдеуі
 (2) болатыны белгілі.
(2) болатыны белгілі.
Осы теңдеу бойынша ізделінді түбірдің келесі жуықтауы жанаманың  осімен қиылысу нүктесі
осімен қиылысу нүктесі  ретінде
ретінде
 (3)
(3)
қатыс арқылы табамыз.
Осы сияқты келесі жуықтаулар да  т.с.с нүктелерде жүргізілген жанамалардың
т.с.с нүктелерде жүргізілген жанамалардың  осімен қиылысыу нүктелері ретінде табылады. Сонда
осімен қиылысыу нүктелері ретінде табылады. Сонда 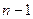 -ші жуықтаудың формуласы
-ші жуықтаудың формуласы
 (4)
(4)
болады. Сонымен бірге 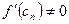 болуын да қарастыру керек. Итерациялық үрдісінің аяқталуы үшін
болуын да қарастыру керек. Итерациялық үрдісінің аяқталуы үшін  шарттың орындалуы немесе екі қатар тұрған жуықтаулардың өте жақын орналасуы, яғни
шарттың орындалуы немесе екі қатар тұрған жуықтаулардың өте жақын орналасуы, яғни  шарттың орындалуы қажет. Сонымен (3) формуладан, Ньютон әдісін қолданғанда есептеулердің көлемі бұрын қарастырылған әдістерге қарағанда көбірек болады, себебі әрбір нүктеде
шарттың орындалуы қажет. Сонымен (3) формуладан, Ньютон әдісін қолданғанда есептеулердің көлемі бұрын қарастырылған әдістерге қарағанда көбірек болады, себебі әрбір нүктеде  функциясының мәнін ғана емес оның туындысының да мәнін табу керек болады, бірақ Ньютон әдісін қолданғанда, басқа әдістерге қарағандағы жинақтылығының жылдамдығы көп болады.
функциясының мәнін ғана емес оның туындысының да мәнін табу керек болады, бірақ Ньютон әдісін қолданғанда, басқа әдістерге қарағандағы жинақтылығының жылдамдығы көп болады.
3. Қателіктерін бағалау.
Енді Ньютон әдісінің жинақтылығы мен оны қолдану туралы кейбір мәселерге тоқтала кетейік.
Бұл жағдайда төмендегі теорема орынды.(оны дәлелдеусіз келтіреміз)
Теорема. Айталық  (1) теңдеудің түбірі, болсын, яғни
(1) теңдеудің түбірі, болсын, яғни  , ал
, ал  болып
болып  үздіксіз бомын. Сонда
үздіксіз бомын. Сонда  түбірді қамтитын
түбірді қамтитын  облыс табылып, егер
облыс табылып, егер  осы облыста жатса, онда Ньютон әдісімен табылған
осы облыста жатса, онда Ньютон әдісімен табылған  мәндердің тізбегі
мәндердің тізбегі  да
да 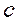 нүктесіне жинақталады.
нүктесіне жинақталады.
Сонымен бірге  қателік үшін
қателік үшін
 қатынас орынды болады.
қатынас орынды болады.
Бұл қатынас әрбір итерацияда қателіктің квадрат дәрежеге шығарылады, яғни түбірдің ойдың белгілерінің шынайы саны екі еселенетінін көрсетеді. Егер

болса, онда  болғанда бес- алты итерациядан кейін қателік
болғанда бес- алты итерациядан кейін қателік  дей болады.
дей болады.
Бұл қазіргі заманғы дәлдігі екі есе артқан ЭЕМ - дердегі қателіктердің ең кіші мүмкін мәні болып есептеледі. Ал осындай дәлдікпен есеп шығару үшін кесіндіні қақ бөлу әдісін қолданғанда итерациялардың саны 50- ден артық болар еді.
Ньютон әдісін қолданудағы бір қиындық бастапқы жуықтаудың  облысында жатуын қамтамасыз ету болып табылады.
облысында жатуын қамтамасыз ету болып табылады.
Сондықтан кейде қосарланған әдісті қолдану тиімді болады, яғни алдымен жинақты болатын бір әдіс (мысалы, кесіндіні қақ бөлу әдісі), ал бірнеше итерациядан кейін тез жинақталатын Ньютон әдісін қолданамыз.
Дәріс №4. Сызықтық алгебралық теңдеулер жүйесін шешудің сандық есебі. Гаусс әдісі.
Жоспар:
Поиск по сайту: