П. 2.1. Табличные математические модели структуры ЗДРАВООХРАНЕНИЯ области

А. Матрица (таблица 2) евклидовых расстояний между объектами/ районами области (лист в альбомном формате на стр. 7).

Пусть исходные данные для многомерной классификации объектов представлены в виде прямоугольной матрицы , , . Её строки – объекты, мерные наблюдения (), подлежащие кластеризации в многомерном пространстве свойств (признаков) на однородные группы, классы, кластеры. Понятие однородности свойств в большинстве методов кластерного анализа определяется через задание меры попарного расстояния (метрики) между любой парой исследуемых объектов . Обычно метрика – это некоторая неотрицательная действительная функция, определённая на множестве , , иудовлетворяющая следующим трём свойствам:

; ;

;

.

В проведённом исследовании выбрана евклидова метрика (Euclidean distance) межу многомерными (двумерными) объектами / районами Воронежской области, которая задаётся формулой

,

где 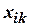– значение ого свойства/признака у 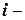го объекта (; ).

Б. Таблица 3 последовательности объединения объектов / районов в кластеры: (лист в альбомном формате на стр.8).

Хотя в иерархическом кластерном анализе не существует формальных критериев, позволяющих однозначно определять оптимальное число классов при структурировании объектов, тем не менее, в нем для предварительного эвристического выявления этого параметра используется таблица последовательности агломераций (слияния) кластеров. Оптимальному числу классов соответствует разность между числом n объектов (в нашем случае n = 33) и порядковым номеромшага, для которого обнаружен первый резкий скачок расстояний между кластерами, фиксируемых в первом столбце таблицы 3. В нашем случае он наблюдается при переходе от 28 шага к 29-му шагу. Поэтому оптимальное число кластеров равно 33-28=5. Тем не менее, выбор окончательного решения о числе кластеров часто зависит от содержательных соображений исследователя. Мы выбрали для практических целей сравнения с построенной ранее одномерной моделью геоинформационной структуры Воронежской области число кластеров, равное пяти.

(далее следуют 2 таблицы на двойных листах в альбомном формате: см. другие файлы)

п.2.2. Дендрограмма как графическая модель
многомерной структуры ЗДРАВООХРАНЕНИЯ районов области

Рис. 1. Горизонтальная дендрограмма обеспеченности медперсоналом
N=33 районных отделов здравоохранения в Воронежской области (С1 – С33).

Замечания. 1) Слева вдоль вертикальной оси указаны номера случаев / объектов (от района с номером С1 до района с номером С33) в общем списке административных районов Воронежской области, перечисленных в столбце «№ района» исходной Таблицы 1. 2) На горизонтальной дендрограмме любое кластерное решение может быть визуально получено путем пересечения её ветвей вертикальной линией: число точек её пересечения с деревом соответствует количеству кластеров на текущем этапе кластеризации. Чтобы выявить состав каждого кластера, необходимо вернуться по ветвям к «корням дерева» и зафиксировать номера/ имена включаемых объектов.

Главный результат исследования. Для поставленной научно-практической междисциплинарной региональной задачи построенная дендрограмма позволяет зафиксировать 5 кластеров по двумерному критерию обеспеченности медицинским персоналом на 10 000 населения: 1) обеспеченность врачами и 2) обеспеченность средним медицинским персоналом. Зафиксируем их, указывая для каждого кластера средний арифметический показатель (индекс) 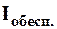обеспеченности населения медиками на 10 000 жителей. При вычислении 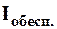для каждого кластера использовалась таблица 4 (см. ниже).

I кластер – двухэлементный. Онвключает в себя два районных отдела здравоохранения: Новоусманский и Каширский. Для него индекс 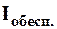обеспеченности населения медперсоналом равен 38, 425 на 10 000 жителей.

II кластер – шестиэлементный. В него входят следующие 6 районных отделов здравоохранения: Богучарский, Верхнехавский, Павловский, Новохопёрский, Панинский, Хохольский. Для него индекс 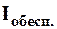обеспеченности населения медперсоналом равен 48, 625 на 10 000 жителей.

III кластер включает в себя следующие 14 районных отделов здравоохранения: Аннинский, Бобровский, Нижнедевицкий, Ольховатский, Таловский, Рамонский, Семилукский, Каменский, Кантемировский, Подгоренский, Эртильский, Петропавловский, Терновский и Борисоглебский городской округ. Для него индекс 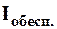обеспеченности населения медперсоналом равен 57,621 на 10 000 жителей.

IV кластер – десятиэлементный. В него входят следующие 10 районных отделов здравоохранения: Бутурлиновский, Острогожский, Репьёвский, Верхнемамонский, Калачеевский, Поворинский, Воробьёвский, Грибановский, Лискинский, Россошанский. Для него индекс 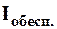обеспеченности населения медперсоналом равен 64,54 на 10 000 жителей.

V кластер – одноэлементный. Он включает в себя лишь один объект – городской отдел здравоохранения городского округа г. Воронеж. Здесь индекс 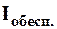обеспеченности населения медперсоналом равен 105,20 на 10 000 жителей.

Таблица 4. Средние показатели обеспеченности районов области

Поиск по сайту: