Абсолютные и относительные показатели изменения структуры

Развитие статистической совокупности проявляется не только в количественном росте или уменьшении элементов системы, но также и в изменении ее структуры. Структура – это строение совокупности, состоящее из отдельных элементов и связей между ними. Например, экспорт страны (совокупность) состоит из различных видов товаров (элементов), стоимость которых различается по видам и по странам. Кроме того, происходит постоянное изменение структуры экспорта в динамике. Соответственно возникает задача изучения структуры совокупностей и их динамики, для чего разработаны специальные методы, которые будут рассмотрены далее.

В теме 2 был рассмотрен индекс структуры, рассчитываемый по формуле (6), который характеризует долю отдельных элементов в итоге абсолютного признака совокупности. В теме 3 рассмотрена система показателей и методика анализа распределения совокупности по значениям какого-либо отдельного признака (вариационный ряд распределения). Здесь излагаются показатели, характеризующие изменение структуры в целом, т.е. «структурный сдвиг» [27]. Практическое применение этих показателей рассмотрим на двух примерах, представленных в таблицах 19 и 20 (первые 4 столбца, выделенные полужирным шрифтом, – исходные данные, а остальные – вспомогательные расчеты).

Таблица 19. Распределение населения России по величине среднедушевых денежных доходов (СДД)

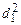
№ группы (j)	СДД, руб./чел. в месяц	Доли населения	| d 1– d 0|			(d 1– d 0)2	(d 1+ d 0)2
2005 год (d 0)	2006 год (d 1)
	до 1500	0,032	0,018	0,014	0,0010	0,0003	0,0002	0,0025	0,0784
	1500-2500	0,088	0,058	0,030	0,0077	0,0034	0,0009	0,0213	0,0422
	2500-3500	0,113	0,085	0,028	0,0128	0,0072	0,0008	0,0392	0,0200
	3500-4500	0,114	0,094	0,020	0,0130	0,0088	0,0004	0,0433	0,0092
	4500-6000	0,149	0,135	0,014	0,0222	0,0182	0,0002	0,0807	0,0024
	6000-8000	0,149	0,149	0,000	0,0222	0,0222	0,0000	0,0888	0,0000
	8000-12000	0,174	0,197	0,023	0,0303	0,0388	0,0005	0,1376	0,0038
	более 12000	0,181	0,264	0,083	0,0328	0,0697	0,0069	0,1980	0,0348
	Итого	1,000	1,000	0,212	0,1420	0,1687	0,0099	0,6114	0,1909

Таблица 20. Распределение численности безработных России по уровню образования в 2006 г.

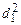
№ группы (j)	Имеют образование	Мужчины (d 0)	Женщины (d 1)	| d 1– d 0|			(d 1– d 0)2	(d 1+ d 0)2
	Высшее профессиональное	0,087	0,130	0,043	0,0076	0,0169	0,0018	0,0471	0,0393
	Неполное высшее профессиональное	0,019	0,023	0,004	0,0004	0,0005	0,0000	0,0018	0,0091
	Сpеднее профессиональное	0,130	0,221	0,091	0,0169	0,0488	0,0083	0,1232	0,0672
	Начальное профессиональное	0,200	0,149	0,051	0,0400	0,0222	0,0026	0,1218	0,0214
	Сpеднее (полное) общее	0,398	0,338	0,060	0,1584	0,1142	0,0036	0,5417	0,0066
	Основное общее	0,148	0,121	0,027	0,0219	0,0146	0,0007	0,0724	0,0101
	Начальное общее, не имеют образ-я	0,018	0,018	0,000	0,0003	0,0003	0,0000	0,0013	0,0000
	Итого	1,000	1,000	0,276	0,2455	0,2177	0,0171	0,9092	0,1536

Обобщающим абсолютным показателем изменения структуры может служить сумма модулей абсолютных изменений долей, определяемая по формуле (50):

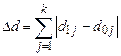, (50)

где d _{1 j} – доля j-ой группы элементов в отчетном периоде; d _{0 j} – доля j-ой группы элементов в базисном периоде.

По данным таблицы 19 в 5-м столбце произведен расчет по формуле (50): =0,212, то есть суммарное изменение долей в распределении россиян по доходам составило 21,2%. Аналогично по той же формуле по данным таблицы 20: =0,276, то есть различие структуры безработных среди женщин и мужчин по уровню образованию составляет 27,6%.

Расчет среднего абсолютного изменения, приходящегося на одну долю (группу, элемент совокупности) не дает никакой дополнительной информации. Зато можно определить, насколько сильно произошедшее изменение структуры в сравнении с предельно возможной величиной суммы модулей, которая равна 2. Для этого используется показатель степени интенсивности абсолютного сдвига (или индекс Лузмора-Хэнби), который определяется по формуле (51):

. (51)

По данным таблицы 19 по формуле (51): =0,106, то есть интенсивность изменения долей в распределении россиян по доходам составила 10,6% от максимально возможного. Аналогично по той же формуле по данным таблицы 20: =0,138, то есть различие структуры безработных среди женщин и мужчин по уровню образованию составляет 13,8% от максимально возможного.

Обобщенная оценка степени структуризации явления в целом обычно выполняется по формуле уровня концентрации (или коэффициент Герфиндаля), который более чувствителен к изменению долей групп с наибольшим удельным весом в итоге, определяемый по формуле (52):

(52)

где – доля -го объекта в общем итоге изучаемого показателя; k – количество объектов.

По данным таблицы 19 в 6-м и 7-м столбцах произведен расчет коэффициента Герфиндаля по формуле (52): H ₂₀₀₅=0,142 и H ₂₀₀₆=0,1687, то есть уровень концентрации в распределении россиян по доходам увеличился в 2006 году по сравнению с 2005 годом. Аналогично по той же формуле по данным таблицы 20: H _муж=0,2455 и H _жен=0,2177, то есть уровень концентрации в распределении безработных по уровню образованию среди мужчин выше, чем среди женщин (влияние уровня образования на статус безработного среди мужчин выше, чем среди женщин).

Обратная индексу Герфиндаля величина – это эффективное число групп в структуре, которое показывает количество групп без учета групп, имеющих ничтожно малые доли, определяется по формуле (53):

E = 1 /H. (53)

По данным таблицы 19 эффективное число групп по формуле (53): E ₂₀₀₅=1/0,142=7,0 и E ₂₀₀₆=5,9, то есть эффективное число групп в распределении россиян по доходам уменьшилось с 7 в 2005 году до 6 в 2005 году, что свидетельствует о необходимости пересмотра интервалов распределения россиян по доходам в будущем году. Аналогично по той же формуле по данным таблицы 20: E _муж=1/0,2455=4,07 и E _жен=1/0,2177=4,59, то эффективное число групп в распределении безработных по уровню образованию среди мужчин выше и среди женщин – 4 у мужчин и 5 у женщин.

Еще один вариант оценки степени структуризации явления в целом – индекс Грофмана (54), который представляет собой сумму модулей абсолютных изменений долей, приходящихся на одну эффективную группу:

. (54)

По данным таблицы 19 в по формуле (54): =0,212*0,142=0,030, то есть изменение долей, приходящихся на одну эффективную группу в распределении россиян по доходам незначительно (3,0%). Аналогично по той же формуле по данным таблицы 20: =0,2455*0,276=0,068, то есть различие структуры в расчете на одну эффектиную группу среди безработных женщин и мужчин по уровню образованию слабое (6,8%).

Для оценки изменений двух наибольших долей (доминантные доли) применяется индекс Липхарта (55):

. (55)

где d _{1 m} и d _{0 m} – доля m -ой группы элементов в отчетном периоде и базисном периодах; m – максимальная доля в совокупности.

По данным таблицы 19 по формуле (55): =0,5*(0,083+0,023)=0,053, то есть среднее изменение долей в двух доминантных группах распределения россиян по доходам составило 5,3%. Аналогично по той же формуле по данным таблицы 20: =0,5*(0,060+0,051)=0,056, то есть различие структуры в двух доминантных группах среди безработных женщин и мужчин по уровню образованию составляет 5,6%.

Рассмотренные показатели основаны на средней арифметической в различных вариантах, и из-за их линейности по отклонениям они одинаково учитывают большие и малые отклонения. Квадратические индексы позволяют сравнивать различные структуры, неразличимые с точки зрения суммы изменений.

Квадратический индекс структурных сдвигов Казинца (56):

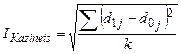. (56)

По данным таблицы 19 по формуле (56): 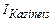= =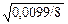0,035, то есть среднее измененение долей в группе в распределении россиян по доходам составило 3,5% (незначительно). Аналогично по той же формуле по данным таблицы 20: 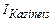= =0,049, то есть различие в группах в структуре безработных среди женщин и мужчин по уровню образованию составляет 4,9% (несущественно).

Аналогичен индексу Казинца индекс наименьших квдратов (или индекс Галлахера), при расчете которого, в отличие от формулы (51), малые разности долей слабее влияют на индекс, чем большие, определяется по формуле (57)[28]:

. (57)

По данным таблицы 19 по формуле (57): 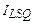= =0,070, то есть интенсивность изменения долей в распределении россиян по доходам составила 7,0%. Аналогично по той же формуле по данным таблицы 20: 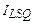= =0,092, то есть различие структуры безработных среди женщин и мужчин по уровню образованию составляет 9,2%.

Незначительную модификацию индекса наименьших квадратов представляет индекс Монро (58):

. (58)

По данным таблицы 19 по формуле (58): = =0,093, то есть интенсивность изменения долей в распределении россиян по доходам по формуле Монро составила 9,3%. Аналогично по той же формуле по данным таблицы 20: = =0,117, то есть различие структуры безработных среди женщин и мужчин по уровню образованию по формуле Монро составляет 11,7%.

Интегральный коэффициент структурных сдвигов Гатева (59), который различает структуры с равными суммами квадратов отклонений (принимает более высокие значения, когда группы имеют примерно одинаковые доли):

. (59)

По данным таблицы 19 по формуле (59): = =0,179, то есть интенсивность изменения долей в распределении россиян по доходам по методике Гатева составила 17,9% (незначительно). Аналогично по той же формуле по данным таблицы 20: = =0,192, то есть различие структуры безработных среди женщин и мужчин по уровню образованию по методике Гатева составляет 19,2% (незначительно).

Индекс Рябцева, отличающийся от (59) только знаменателем, принимает обычно более низкие значения, рассчитывается по формуле (60):

. (60)

По данным таблицы 19 по формуле (60): = =0,127, то есть интенсивность изменения долей в распределении россиян по доходам по методике Рябцева составила 12,7% (незначительно). Аналогично по той же формуле по данным таблицы 20: = =0,137, то есть различие структуры безработных среди женщин и мужчин по уровню образованию по методике Рябцева составляет 13,7% (достаточно значительно).

Индекс структурных различий Салаи (61), особенноситью которого является то, что чем больше доля j -ой группы, тем большее значение будет принимать ², что ведет к уменьшению вклада j -ой группы в общей сумме, тем самым увеличивая значимость изменения долей малых групп:

(61)

По данным таблицы 19 по формуле (61): = =0,154, то есть средняя интенсивность изменения долей в распределении россиян по доходам по методике Салаи составила 15,4%. Аналогично по той же формуле по данным таблицы 20: = =0,148, то есть среднее различие долей в группах безработных среди женщин и мужчин по уровню образованию по методике Салаи составляет 14,8%.

Для оценки структуры распределения доходов применяются специфические индексы: индекс Джини, индекс Аткинсона, индекс обобщенной энтропии, которые будут рассмотрены в курсе социально-экономической статистики в теме «Статистика уровня жизни».

Поиск по сайту: