Проверка соответствия ряда распределения нормальному

Под теоретической кривой распределения понимается графическое изображение ряда в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариантов, другими словами, теоретическое распределение может быть выражено аналитически – формулой, которая связывает частоты и соответствующие значения признака. Такие алгебраические формулы носят название законов распределения. Большое познавательное значение имеет сопоставление фактических кривых распределения с теоретическими.

Как уже неоднократно отмечалось, часто пользуются типом распределения, которое называется нормальным. Формула функции плотности нормального распределения имеет следующий вид (41):

или (41)

где X – значение изучаемого признака;

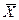– средняя арифметическая ряда;

σ – среднее квадратическое отклонение;

– нормированное отклонение;

π = 3,1415 – постоянное число (отношение длины окружности к ее диаметру);

e = 2,7182 – основание натурального логарифма.

Следовательно, кривая нормального распределения может быть построена по двум параметрам – средней арифметической и среднему квадратическому отклонению. Поэтому важно выяснить, как эти параметры влияют на вид нормальной кривой.

Если 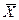не меняется, а изменяется только σ, то чем меньше σ, тем более вытянута вверх кривая и наоборот, чем больше σ, тем более плоской и растянутой вдоль оси абсцисс становится кривая нормального распределения (см. рис. 8).

= const σ1 < σ2 < σ3

Рис. 8. Влияние величины σ на кривую нормального распределения

Если σ остается неизменной, а 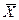изменяется, то кривые нормального распределения имеют одинаковую форму, но отличаются друг от друга положением максимальной ординаты (вершины) (см. рис. 9).

< <

Рис. 9. Влияние величины 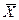на кривую нормального распределения

Итак, выделим особенности кривой нормального распределения:

1) кривая симметрична и имеет максимум в точке, соответствующей значению 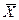= Ме = Мо;

2) кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности (чем больше отдельные значения X отклоняются от 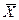, тем реже они встречаются);

3) кривая имеет две точки перегиба на расстоянии ± σ от ;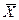

4) коэффициенты асимметрии и эксцесса равны нулю.

Гипотезы о распределениях заключаются в том, что выдвигается предположение о том, что распределение в изучаемой совокупности подчиняется какому-то определенному закону. Проверка гипотезы состоит в том, чтобы на основании сравнения фактических (эмпирических) частот с предполагаемыми (теоретическими) частотами сделать вывод о соответствии фактического распределения гипотетическому распределению.

Под гипотетическим распределением необязательно понимается нормальное распределение. Может быть выдвинута гипотеза о логнормальном, биномиальном распределениях, распределении Пуассона и пр.[21] Причина частого обращения к нормальному распределению состоит в том, что, как уже было замечено ранее, в этом типе распределения выражается закономерность, возникающая при взаимодействии множества случайных причин, когда ни одна из не имеет преобладающего влияния.

В нашем примере про ВО близость значений средней арифметической величины (60,82), медианы (59,30) и моды (58,96) указывает на вероятное соответствие изучаемого распределения нормальному закону.

Проверка гипотезы о соответствии теоретическому распределению предполагает расчет теоретических частот этого распределения.

Для нормального распределения порядок расчета этих частот следующий:

1) по эмпирическим данным рассчитывают среднюю арифметическую ряда 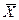и среднее квадратическое отклонение σ;

2) находят нормированное (выраженное в σ) отклонение каждого эмпирического значения от средней арифметической:

;(42)

3) по формуле (41) или с помощью таблиц интеграла вероятностей Лапласа находят значение φ (t)[22];

4) вычисляют теоретические частоты m по формуле:

,(43)

где N – объем совокупности, h_i – длина (размах) i -го интервала.

Определим теоретические частоты нормального распределения в нашем примере про ВО по данным табл. 12, для чего построим вспомогательную таблицу 14. Средняя арифметическая величина и среднее квадратическое отклонение нами уже найдены ранее (); значения нормированных отклонений t рассчитаны в 5-м столбце таблицы 14, а значения плотностей φ (t) – в 8-м столбце (в 6-м и 7-м столбцах приведены промежуточные расчеты по формуле (41)); в последнем столбце – теоретические частоты нормального распределения.

Таблица 14. Расчет теоретических частот нормального распределения

i	Xi	fi	Хi’				φ (t)	mi
	24,16 – 38,66		31,41	-1,4889	-1,1084	0,3301	0,0067	3,383
	38,66 – 53,16		45,91	-0,7549	-0,2850	0,7520	0,0152	7,707
	53,16 – 67,66		60,41	-0,0210	-0,0002	0,9998	0,0202	10,246
	67,66 – 82,16		74,91	0,7130	-0,2542	0,7756	0,0157	7,948
	82,16 – 96,66		89,41	1,4470	-1,0468	0,3510	0,0071	3,598
	96,66 – 111,16		103,91	2,1809	-2,3782	0,0927	0,0019	0,950
	Итого							33,832

Сравним на графике эмпирические f (ВО по таможенным постам) и теоретические m (нормальное распределение) частоты, полученные на основе данных табл. 14 (рис. 10). Близость этих частот очевидна[23], но объективная оценка их соответствия может быть получена только с помощью критериев согласия.

Рис. 10. Распределение ВО по таможенным постам (эмпирическое) и нормальное

Критерии согласия, опираясь на установленный закон распределения, дают возможность установить, когда расхождения между теоретическими и эмпирическими частотами следует признать несущественными (случайными), а когда – существенными (неслучайными). Таким образом, критерии согласия позволяют отвергнуть или подтвердить правильность выдвинутой гипотезы о характере распределения в эмпирическом ряду и дать ответ, можно ли принять для данного эмпирического распределения модель, выраженную некоторым теоретическим законом распределения.

Существует ряд критериев согласия, но чаще всего применяют критерии Пирсона χ², Колмогорова и Романовского.

Критерий согласия Пирсона χ² (хи-квадрат) – один из основных критериев согласия, рассчитываемый по формуле (44):

, (44)

где k – число интервалов;

f_i – эмпирическая частота i -го интервала;

m_i – теоретическая частота.

Для распределения χ² составлены таблицы, где указано критическое значение критерия согласия χ² для выбранного уровня значимости α и данного числа степеней свободы ν (см. Приложение 3).

Уровень значимости α – это вероятность ошибочного отклонения выдвинутой гипотезы, т.е. вероятность (P) того, что будет отвергнута правильная гипотеза. В статистических исследованиях в зависимости от важности и ответственности решаемых задач пользуются следующими тремя уровнями значимости:

1) α = 0,10, тогда P = 0,90;

2) α = 0,05, тогда P = 0,95 [24];

3) α = 0,01, тогда P = 0,99.

Число степеней свободы ν определяется по формуле:

ν = k – z – 1,(45)

где k – число интервалов;

z – число параметров, задающих теоретический закон распределения.

Для нормального распределения z = 2, так как нормальное распределение зависит от двух параметров – средней арифметической (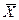) и среднего квадратического отклонения (σ).

Для оценки существенности расхождений расчетное значение χ² сравнивают с табличным χ² _табл. Расчетное значения критерия должно быть меньше табличного, т.е. χ²<χ² _табл, в противном случае расхождения между теоретическим и эмпирическим распределением не случайны, а теоретическое распределение не может служить моделью для изучаемого эмпирического распределения.

Использование критерия χ² рекомендуется для достаточно больших совокупностей (N >50), при этом частота каждой группы не должна быть менее 5, в противном случае повышается вероятность получения ошибочных выводов.

В нашем примере про ВО для расчета критерия χ² построим вспомогательную таблицу 15.

Таблица 15. Вспомогательные расчеты критериев согласия

i	Xi	fi	mi		fi’	mi’	|fi’– mi’|
	24,16 – 38,66		3,383	0,773		3,383	1,617
	38,66 – 53,16		7,707	0,065		11,090	0,910
	53,16 – 67,66		10,246	0,740		21,336	3,664
	67,66 – 82,16		7,948	1,961		29,284	0,284
	82,16 – 96,66		3,598	0,045		32,882	0,118
	96,66 – 111,16		0,950	1,160		33,832	1,168
	Итого		33,832	4,744

Теперь по формуле (44): χ² =4,744, что меньше табличного (Приложение 3) значения χ² _табл=7,8147 при уровне значимости α = 0,05 и числе степеней свободы ν= 6–2–1=3, значит с вероятностью 0,95 можно говорить, что в основе эмпирического распределения величины ВО по таможенным постам лежит закон нормального распределения, т.е. выдвинутая гипотеза не отвергается, а расхождения объясняются случайными факторами.

Критерий Романовского К_Р основан на использовании критерия Пирсона χ ², т.е. уже найденных значений χ ² и числа степеней свободы ν, рассчитывается по формуле (46):

. (46)

Он используется в том случае, когда отсутствует таблица значений χ ². Если К_Р < 3, то расхождения между теоретическим и эмпирическим распределением случайны, если К_Р > 3, то не случайны, и теоретическое распределение не может служить моделью для изучаемого эмпирического распределения.

В нашем примере про ВО по формуле (46): = 0,712 < 3, что подтверждает несущественность расхождений между эмпирическими и теоретическими частотами.

Критерий Колмогорова λ основан на определении максимального расхождения между накопленными частотами эмпирического и теоретического распределений (D), рассчитывается по формуле (47) [25]:

. (47)

Рассчитав значение λ, по таблице P (λ) (см. Приложение 6) определяют вероятность, с которой можно утверждать, что отклонения эмпирических частот от теоретических случайны. Вероятность P (λ) может изменяться от 0 до 1. При P (λ) = 1 (т.е. при λ < 0,3) происходит полное совпадение частот, при P (λ) = 0 – полное расхождение.

В нашем примере про ВО в последних трех столбцах таблицы 15 приведены расчеты накопленных частот и разностей между ними, откуда видно, что в 3-ей группе наблюдается максимальное расхождение (разность) D = 3,664. Тогда по формуле (47): . По таблице Приложения 6 находим значение вероятности при λ = 0,6: P = 0,86 (наиболее близкое значение к 0,619), т.е. с вероятностью, близкой к 0,86, можно говорить, что в основе эмпирического распределения величины ВО по таможенным постам лежит закон нормального распределения, а расхождения эмпирического и теоретического распределений носят случайный характер.

Итак, подтвердив правильность выдвинутой гипотезы с помощью известных критериев согласия, можно использовать результаты распределения для практической деятельности. Какое же практическое значение может иметь произведенная проверка гипотезы? Во-первых, соответствие нормальному закону позволяет прогнозировать, какое число таможенных постов (или их доля) попадет в тот или иной интервал значений величины ВО. Во-вторых, нормальное распределение возникает при действии на вариацию изучаемого показателя множества независимых факторов. Из чего следует, что нельзя существенно снизить вариацию величины ВО, воздействуя только на один-два управляемых фактора, скажем число работников таможенного поста или степень технической оснащенности.

Поиск по сайту: