Алгоритм открытого распределения ключей Диффи - Хеллмана

Проблема распределения ключей была решена в той же основополагающей работе Диффи и Хеллмана, где разработана схема шифрования с открытым ключом. Их протокол распределения ключей, названный протоколом Диффи - Хеллмана обмена ключей, позволяет двум сторонам достигнуть соглашения о секретном ключе по открытому каналу связи без предварительной личной встречи. Его стойкость основывается на трудноразрешимой проблеме дискретного логарифмирования в конечной абелевой группе А.

В своей работе авторы предлагали использовать группу А — но на сегодняшний день многие эффективные версии этого протокола берут за основу группу эллиптической кривой. Такие версии обозначают аббревиатурой EC-DH, возникшей от сокращений английских терминов: Elliptic Curve и Diffie-Hellman. Основные сообщения в протоколе Диффи - Хеллмана представлены следующей диаграммой1:

Каждая из сторон обладает своим кратковременным секретным ключом а и b соответственно, с помощью которых они могут договориться об общем сеансовом ключе:

- Алиса может вычислить k = поскольку она знает а и посланное Бобом сообщение

- Боб тоже может определить k = поскольку ему известно b, а 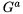он узнает от Алисы.

Атакующая Ева может перехватить сообщения и и попытаться восстановить секретный ключ, равный к = что является в точности задачей Диффи - Хеллмана, рассмотренной в главе 7. Следовательно, криптостойкость этого протокола основывается не на дискретном логарифмировании, а на сложности решения задачи Диффи - Хеллмана. Напомним, что, возможно, задача Диффи-Хеллмана более легкая, чем дискретное логарифмирование, хотя в это с трудом верится, когда речь идет о группах, традиционно используемых в реальных протоколах.

Обратите внимание на то, что протокол Диффи - Хеллмана может нормально работать и в режиме онлайн (когда обе стороны вносят свои поправки в вырабатываемый ключ), и в режиме оффлайн (когда один из партнеров использует долговременный ключ вида вместо кратковременного). Значит, с помощью протокола Диффи - Хеллмана можно как договариваться о ключах, так и менять их.

Приведем простой пример. Заметим, что для практических целей выбирают с Р ≈ 21024, но мы в качестве параметров возьмем

Р = 2147483659 и G = 2.

На диаграмме изображен возможный обмен сообщениями в протоколе Диффи - Хеллмана:

Общий ключ вычисляется по формулам:

(mod P) = 1333327162, (mod P) = 1333327162. Обратите внимание на то, что в протоколе передаются элементы выбранной абелевой группы. Следовательно, при использовании затраты на передачи составят около 1024 бит в каждом направлении, поскольку Р ≈ . Однако если используется группа эллиптической кривой 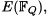можно брать Q ≈ 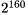и снизить затраты на передачу сообщений до 160 бит на сообщение. Кроме того, возведение в степень на эллиптической кривой осуществляется более эффективно, чем в числовом поле.

Для «игрушечного» примера протокола EC-DH возьмем эллиптическую кривую, задаваемую уравнением

Е : = + X - 3

над полем 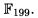Пусть элемент G имеет координаты (1,76). Тогда возможные сообщения протокола имеют вид:

Общим ключом служит Х-координата точки, вычисляемой следующим образом:

[b]А = [86](2,150) = (156,75), [а]В = [23](123,187) = (156,75).

Общий ключ здесь — 156. Кроме того, вместо полной точки кривой можно передавать сжатую точку, что существенным образом скажется на времени передачи.

Итак, задача распределения ключей кажется решенной. Однако остается важная проблема: откуда Вы знаете с кем Вы договариваетесь о сеансовом ключе? У Алисы нет оснований для уверенности, что она переписывается именно с Бобом. Это может привести к следующей атаке, которая условно называется «человек посередине»:

При этом

- Алиса договаривается о ключе с Евой, думая, что переписывается с Бобом;

- Боб ведет переговоры о ключе с Евой, считая, что его корреспондент — Алиса;

- Ева может изучать сообщения, т.к. они проходят через нее как через коммутатор. Поскольку она не вносит изменений в открытый текст, ее действия не могут быть обнаружены.

Итак, можно сделать вывод о том, что самого по себе протокола Диффи - Хеллмана не достаточно для обеспечения секретности распределения ключей.

Поиск по сайту: