Алгоритм RSA

RSA (аббревиатура от фамилий Rivest, Shamir и Adleman) — криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел.

RSA-ключи генерируются следующим образом:

8. Выбираются два различных случайных простых числа и заданного размера (например, 1024 бита каждое).

9. Вычисляется их произведение , которое называется модулем.

10. Вычисляется значение функции Эйлера от числа :

11. Выбирается целое число (), взаимно простое со значением функции . Обычно в качестве берут простые числа, содержащие небольшое количество единичных бит в двоичной записи, например, простые числа Ферма 17, 257 или 65537.

· Число называется открытой экспонентой (англ. public exponent)

· Время, необходимое для шифрования с использованием быстрого возведения в степень, пропорционально числу единичных бит в .

· Слишком малые значения , например 3, потенциально могут ослабить безопасность схемы RSA.^[15]

12. Вычисляется число , мультипликативно обратное к числу по модулю , то есть число, удовлетворяющее условию:

· Число называется секретной экспонентой. Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.

13. Пара 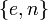публикуется в качестве открытого ключа RSA (англ. RSA public key).

14. Пара играет роль закрытого ключа RSA (англ. RSA private key) и держится в секрете.

]Шифрование и расшифрование

Предположим, Боб хочет послать Алисе сообщение .

Сообщениями являются целые числа в интервале от 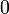до , т.е .

Поиск по сайту: