Билет № 38

Простой и обобщенный алгоритмы Эвклида.

Алгори́тм Евкли́да — алгоритм для нахождения наибольшего общего делителя двух целых чисел.

Алгоритм Евклида для целых чисел

Пусть и — целые числа, не равные одновременно нулю, и последовательность чисел

определена тем, что каждое — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть

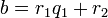
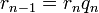
Тогда НОД(a, b), наибольший общий делитель и , равен 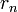, последнему ненулевому члену этой последовательности.

Существование таких 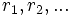, то есть возможность деления с остатком на для любого целого и целого , доказывается индукцией по m.

Корректность этого алгоритма вытекает из следующих двух утверждений:

Пусть , тогда НОД (a, b) = НОД (b, r).

Доказательство [показать]

НОД(0, ) = для любого ненулевого (т.к. 0 делится на любое целое число, кроме нуля).

Проще сформулировать алгоритм Евклида так: если даны натуральные числа и и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.

Расширенный алгоритм Евклида и соотношение Безу

Основная статья: Соотношение Безу

Формулы для могут быть переписаны следующим образом:

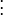
НОД

здесь s и t целые. Это представление наибольшего общего делителя называется соотношением Безу, а числа s и t — коэффициентами Безу. Соотношение Безу является ключевым в доказательстве леммы Евклида и основной теоремы арифметики.

Связь с цепными дробями

Отношение допускает представление в виде цепной дроби:

.

При этом цепная дробь без последнего члена равна отношению коэффициентов Безу , взятому со знаком минус:

.

Последовательность равенств, задающая алгоритм Евклида может быть переписана в форме

Последнее слагаемое в правой части равенства всегда равно обратному значению левой части следующего уравнения. Поэтому первые два уравнения могут быть объединены в форме

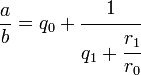
Третье равенство может быть использовано чтобы заменить знаменатель выражения r ₁/ r ₀, получим

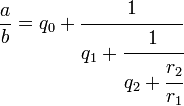
Последнее отношение остатков r_k / r_{k −1} всегда может быть заменено используя следующее равенство в последовательности, и так до последнего уравнения. Результатом является цепная дробь

В приведённом выше примере, НОД(1071, 462) было посчитано и были найдены частные q_k 2,3 и 7 соответственно. Поэтому, 1071/462 может быть записана как

Вариации и обобщения

Кольца, в которых применим алгоритм Евклида, называются евклидовыми кольцами. К ним относятся, в частности, кольца многочленов.

Обобщённый алгоритм Евклида для многочленов

Алгоритм Евклида и расширенный алгоритм Евклида естественным образом обобщается на кольцо многочленов k [ x ] от одной переменной над произвольным полем k, поскольку для таких многочленов определена операция деления с остатком. При выполнении алгоритма Евклида для многочленов аналогично алгоритму Евклида для целых чисел, получается последовательность полиномиальных остатков (PRS).

Пример для кольца Z [ x ]

Пусть cont(f) по определению — НОД коэффициентов многочлена f(x) из Z[x] — содержание многочлена. Частное от деления f(x) на cont(f) называется примитивной частью многочлена f(x) и обозначается primpart(f(x)).

эти определения понадобятся для нахождения НОД двух многочленов p1(x) и p2(x) в кольце Z[x]. Для многочленов над целыми числами верно следующее:

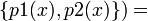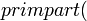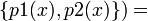НОД НОД , НОД НОД .

Таким образом задача отыскания НОД двух произвольных многочленов сводится к задаче отыскания НОД примитивных полиномов.

Пусть есть два примитивных многочлена p1(x) и p2(x) из Z[x], для которых выполняется соотношение между их степенями: deg(p1(x)) = m и deg(p2(x)) = n, m > n. Деление многочленов с остатком предполагает точную делимость старшего коэффициента делимого на старший коэффициент делителя, в общем случае деление с остатком выполнить невозможно. Поэтому вводят алгоритм псевдоделения, который всё же позволяет получить псевдочастное и псевдоостаток (prem), которые будут сами по себе принадлежать множеству многочленов над целыми числами.

Под псевдоделением будем понимать, что самому делению предшествует умножение полинома p1(x) на , то есть , , где и — соответственно псевдочастное и псевдоостаток.

Итак, — (принадлежат кольцу многочленов над целыми числами), причём . Тогда алгоритм Евклида состоит из следующих шагов:

1. Вычисление НОД содержаний:

НОД .

2. Вычисление примитивных частей:

.

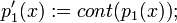
3. Построение последовательности полиномиальных остатков:

.

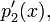
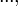
4. Выход и возврат результата:

Если , то вернуть , иначе вернуть .

Ускоренные версии алгоритма

Одним из методов ускорения целочисленного алгоритма Евклида является использование симметричного остатка:

где

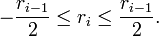
Одна из версий ускоренного алгоритма Евклида для полиномов основывается на том, что промежуточные значения алгоритма в основном зависят от высоких степеней. Применение стратегии Разделяй и Властвуй позволяет уменьшить асимптотическую сложность алгоритма.

Пото́чный шифр — это симметричный шифр, в котором каждый символ открытого текста преобразуется в символ шифрованного текста в зависимости не только от используемого ключа, но и от его расположения в потоке открытого текста. Поточный шифр реализует другой подход к симметричному шифрованию, нежели блочные шифры.

Классификация поточных шифров

Допустим, например, что в режиме гаммирования для поточных шифров при передаче по каналу связи произошло искажение одного знака шифротекста. Очевидно, что в этом случае все знаки, принятые без искажения, будут расшифрованы правильно. Произойдёт потеря лишь одного знака текста. А теперь представим, что один из знаков шифротекста при передаче по каналу связи был потерян. Это приведёт к неправильному расшифрованию всего текста, следующего за потерянным знаком.
Практически во всех каналах передачи данных для поточных систем шифрования присутствуют помехи. Поэтому для предотвращения потери информации решают проблему синхронизации шифрования и расшифрования текста. По способу решения этой проблемы шифросистемы подразделяются на синхронные и системы с самосинхронизацией.

Синхронные поточные шифры

Определение:

Синхронные поточные шифры (СПШ) — шифры, в которых поток ключей генерируется независимо от открытого текста и шифротекста.

При шифровании генератор потока ключей выдаёт биты потока ключей, которые идентичны битам потока ключей при дешифровании. Потеря знака шифротекста приведёт к нарушению синхронизации между этими двумя генераторами и невозможности расшифрования оставшейся части сообщения. Очевидно, что в этой ситуации отправитель и получатель должны повторно синхронизоваться для продолжения работы.

Обычно синхронизация производится вставкой в передаваемое сообщение специальных маркеров. В результате этого пропущенный при передаче знак приводит к неверному расшифрованию лишь до тех пор, пока не будет принят один из маркеров.

Заметим, что выполняться синхронизация должна так, чтобы ни одна часть потока ключей не была повторена. Поэтому переводить генератор в более раннее состояние не имеет смысла.

Плюсы СПШ:

отсутствие эффекта распространения ошибок (только искажённый бит будет расшифрован неверно);

предохраняют от любых вставок и удалений шифротекста, так как они приведут к потере синхронизации и будут обнаружены.

Минусы СПШ:

уязвимы к изменению отдельных бит шифрованного текста. Если злоумышленнику известен открытый текст, он может изменить эти биты так, чтобы они расшифровывались, как ему надо.

Самосинхронизирующиеся поточные шифры

Основная идея построения была запатентована в 1946 г. в США.
Определение:
Самосинхронизирующиеся поточные шифры (асинхронные поточные шифры (АПШ)) – шифры, в которых поток ключей создаётся функцией ключа и фиксированного числа знаков шифротекста.

Итак, внутреннее состояние генератора потока ключей является функцией предыдущих N битов шифротекста. Поэтому расшифрующий генератор потока ключей, приняв N битов, автоматически синхронизируется с шифрующим генератором.
Реализация этого режима происходит следующим образом: каждое сообщение начинается случайным заголовком длиной N битов; заголовок шифруется, передаётся и расшифровывается; расшифровка является неправильной, зато после этих N бит оба генератора будут синхронизированы.

Плюсы АПШ:

Размешивание статистики открытого текста. Так как каждый знак открытого текста влияет на следующий шифротекст, статистические свойства открытого текста распространяются на весь шифротекст. Следовательно, АПШ может быть более устойчивым к атакам на основе избыточности открытого текста, чем СПШ.

Минусы АПШ:

распространение ошибки (каждому неправильному биту шифротекста соответствуют N ошибок в открытом тексте);

чувствительны к вскрытию повторной передачей.

Блочный шифр — разновидность симметричного шифра ^[1], оперирующего группами бит фиксированной длины — блоками, характерный размер которых меняется в пределах 64 — 256 бит. Если исходный текст (или его остаток) меньше размера блока, перед шифрованием его дополняют. Фактически, блочный шифр представляет собой подстановку на алфавите блоков, которая, как следствие, может быть моно- или полиалфавитной. ^[2] Блочный шифр является важной компонентой многих криптографических протоколов и широко используется для защиты данных, передаваемых по сети.

В отличие от шифроблокнота, где длина ключа равна длине сообщения, блочный шифр способен зашифровать одним ключом одно или несколько сообщений, суммарной длиной больше, чем длина ключа. Передача малого по сравнению с сообщением ключа по зашифрованному каналу — задача значительно более простая и быстрая, чем передача самого сообщения или ключа такой же длины, что делает возможным его повседневное использование. Однако, при этом шифр перестает быть невзламываемым. От поточных шифров работа блочного отличается обработкой бит группами, а не потоком. При этом блочные шифры надёжней, но медленее поточных. ^[3] Симметричные системы обладают преимуществом над асимметричными в скорости шифрования, что позволяет им оставаться актуальными, несмотря на более слабый механизм передачи ключа (получатель должен знать секретный ключ, который необходимо передать по уже налаженному зашифрованному каналу. В то же время, в асимметричных шифрах открытый ключ, необходимый для шифрования, могут знать все, и нет необходимости в передачи ключа шифрования).

К достоинствам блочных шифров относят сходство процедур шифрования и расшифрования, которые, как правило, отличаются лишь порядком действий. Это упрощает создание устройств шифрования, так как позволяет использовать одни и те же блоки в цепях шифрования и расшифрования. Гибкость блочных шифров позволяет использовать их для построения других криптографических примитивов: генератора псевдослучайной последовательности, поточного шифра, имитовставки и криптографических хэшей. ^[4]

Определение

Блочный шифр состоит из двух парных алгоритмов: шифрования и расшифрования. ^[8] Оба алгоритма можно представить в виде функций. Функция шифрования E (англ. encryption — шифрование) на вход получает блок данных M (англ. message — сообщение) размером n бит и ключ K (англ. key — ключ) размером k бит и на выходе отдает блок шифротекста C (англ. cipher — шифр) размером n бит:

Для любого ключа K, E_K является биективной функцией (перестановкой) на множестве n -битных блоков. Функция расшифрования D (англ. decryption — расшифрование) на вход получает шифр C, ключ K и на выходе отдает M:

являясь, при этом, обратной к функции шифрования:

и

Заметим, что ключ, необходимый для шифрования и дешифрования, один и тот же — следствие симметричности блочного шифра.

Билет № 39

Электро́нная по́дпись (ЭП) — информация в электронной форме, присоединенная к другой информации в электронной форме (электронный документ) или иным образом связанная с такой информацией. Используется для определения лица, подписавшего информацию (электронный документ)[1].

По своему существу электронная подпись представляет собой реквизит электронного документа, позволяющий установить отсутствие искажения информации в электронном документе с момента формирования ЭП и проверить принадлежность подписи владельцу сертификата ключа ЭП. Значение реквизита получается в результате криптографического преобразования информации с использованием закрытого ключа ЭП.

Назначение и применение ЭП

Электронная подпись предназначена для идентификации лица, подписавшего электронный документ и является полноценной заменой (аналогом) собственноручной подписи в случаях, предусмотренных законом[2].

Использование электронной подписи позволяет осуществить:

Контроль целостности передаваемого документа: при любом случайном или преднамеренном изменении документа подпись станет недействительной, потому что вычислена она на основании исходного состояния документа и соответствует лишь ему.

Защиту от изменений (подделки) документа: гарантия выявления подделки при контроле целостности делает подделывание нецелесообразным в большинстве случаев.

Невозможность отказа от авторства. Так как создать корректную подпись можно, лишь зная закрытый ключ, а он должен быть известен только владельцу, то владелец не может отказаться от своей подписи под документом.

Доказательное подтверждение авторства документа: Так как создать корректную подпись можно, лишь зная закрытый ключ, а он должен быть известен только владельцу, то владелец пары ключей может доказать своё авторство подписи под документом. В зависимости от деталей определения документа могут быть подписаны такие поля, как «автор», «внесённые изменения», «метка времени» и т. д.

Алгоритмы

Существует несколько схем построения цифровой подписи:

На основе алгоритмов симметричного шифрования. Данная схема предусматривает наличие в системе третьего лица — арбитра, пользующегося доверием обеих сторон. Авторизацией документа является сам факт зашифрования его секретным ключом и передача его арбитру.[8]

На основе алгоритмов асимметричного шифрования. На данный момент такие схемы ЭП наиболее распространены и находят широкое применение.

Кроме этого, существуют другие разновидности цифровых подписей (групповая подпись, неоспоримая подпись, доверенная подпись), которые являются модификациями описанных выше схем.[8] Их появление обусловлено разнообразием задач, решаемых с помощью ЭП.

1. Прежде чем получить доступ к КС, пользователь должен идентифицировать себя, а затем средства защиты сети должны подтвердить подлинность этого пользователя, т.е. проверить, является ли данный пользователь действительно тем, за кого он себя выдает. Компоненты механизма защиты легальных пользователей размещены на рабочей ЭВМ, к которой подключен пользователь через его терминал (или каким-либо иным способом). Поэтому процедуры идентификации, подтверждения подлинности и наделения полномочиями выполняются в начале сеанса на местной рабочей ЭВМ.

Когда пользователь начинает работу в КС, используя терминал, система запрашивает его имя и идентификационный номер. В зависимости от ответов пользователя компьютерная система проводит его идентификацию. Затем система проверяет, является ли пользователь действительно тем, за кого он себя выдает. Для этого она запрашивает у пользователя пароль. Пароль - это лишь один из способов подтверждения подлинности пользователя.

Перечислим возможные способы подтверждения подлинности.

Предопределенная информация, находящаяся в распоряжении пользователя: пароль, персональный идентификационный номер, соглашение об использовании специальных закодированных фраз.

Элементы аппаратного обеспечения, находящиеся в распоряжении пользователя: ключи, магнитные карточки, микросхемы и т.п.

Характерные личные особенности пользователя: отпечатки пальцев, рисунок сетчатки глаза, тембр голоса и т.п.

Характерные приемы и черты поведения пользователя в режиме реального времени: особенности динамики и стиль работы на клавиатуре, приемы работы с манипулятором и т.п.

Навыки и знания пользователя, обусловленные образованием, культурой, обучением, воспитанием, привычками и т.п.

Применение пароля для подтверждения подлинности пользователя. Традиционно каждый законный пользователь компьютерной системы получает идентификационный номер и/или пароль. В начале сеанса работы на терминале пользователь указывает свой идентификационный номер (идентификатор пользователя) системе, которая затем запрашивает у пользователя пароль.

Рис.1. Схема простой аутентификации с помощью пароля

Простейший метод подтверждения подлинности с использованием пароля основан на сравнении представляемого пользователем пароля РА с исходным значением Р'А, хранящимся в компьютерном центре (рис.1). Поскольку пароль должен храниться в тайне, его следует шифровать перед пересылкой по незащищенному каналу. Если значения РА и Р'А совпадают, то пароль РА считается подлинным, а пользователь - законным. Если кто-нибудь, не имеющий полномочий для входа в систему, узнает каким-либо образом пароль и идентификационный номер законного пользователя, он получит доступ в систему.

Иногда получатель не должен раскрывать исходную открытую форму пароля. В этом случае отправитель должен пересылать вместо открытой формы пароля отображение пароля, получаемое с использованием односторонней функции (·) пароля. Это преобразование должно гарантировать невозможность раскрытия противником пароля по его отображению, так как противник наталкивается на неразрешимую числовую задачу.

Например, функция  (·) может быть определена следующим образом:

(Р) = ЕР(ID),

где Р - пароль отправителя; ID - идентификатор отправителя;

ЕP - процедура шифрования, выполняемая с использованием пароля Р в качестве ключа.

Такие функции особенно удобны, если длина пароля и длина ключа одинаковы. В этом случае подтверждение подлинности с помощью пароля состоит из пересылки получателю отображения (P) и сравнения его с предварительно вычисленным и хранимым эквивалентом '(Р).

На практике пароли состоят только из нескольких букв, чтобы дать возможность пользователям запомнить их. Короткие пароли уязвимы к атаке полного перебора всех вариантов. Для того чтобы предотвратить такую атаку, функцию (Р) определяют иначе,а именно:

 (Р)=ЕPK(ID),

где К и ID - соответственно ключ и идентификатор отправителя.

Очевидно, значение  (Р) вычисляется заранее и хранится в виде '(P) в идентификационной таблице у получателя (рис. 2). Подтверждение подлинности состоит из сравнения двух отображений пароля (РA) и (РA) и признания пароля РA, если эти отображения равны. Конечно, любой, кто получит доступ к идентификационной таблице, может незаконно изменить ее содержимое, не опасаясь, что эти действия будут обнаружены.

Поиск по сайту: