Индексы средних величин

При изучении качественных показателей часто приходится рассматривать изменение во времени (или пространстве) средней величины индексируемого показателя для определенной однородной совкупности. Например, в статистических сборниках публикуются данные о динамике средних цен, средней номинальной заработной плате в отдельных отраслях и т.д.

Средняя величина является обощающей характеристикой качественного показателя и складывается как под влиянием значений показателя у индивидуальных элементов (единиц), из которых состоит объект, так и под влиянием соотношения их весов («структуры» объекта).

Если любой качественный индексируемый показатель обозначить через x, а его веса – через f, то динамику среднего показателя можно отразить как за счет изменения обоих факторов (x и f), так и за счет каждого фактора отдельно. В результате получим 3 различных индекса: индекс переменного состава, индекс фиксированного состава и индекс структурных сдвигов.

Индекс переменного состава отражает динамику среднего показателя (для однородной совокупности) за счет изменения индексируемой величины x у отдельных элементов (частей целого) и за счет изменения весов f, по которым взвешиваются отдельные значения x. Любой индекс переменного состава – это отношение двух средних величин для однородной совокупности (за два периода или по двум территориям) (202):

. (202)

Свое название этот индекс получил потому, что он характеризует динамику средних величин не только за счет изменения индексируемой величины у отдельных элементов (частей целого), но и за счет изменения удельного веса этих частей в общей совокупности, т.е. изменения состава совокупности.

Индекс фиксированного состава отражает динамику среднего показателя лишь за счет изменения индексируемой величины x, при фиксировании весов. Если фиксировать веса на уровне отчетного периода f ₁, то получим формулу самую распространенную[57] формулу индекса фиксированного состава (203):

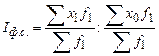. (203)

Другими словами, индекс фиксированного состава исключает влияние структуры (состава) совокупности на динамику средних величин, рассчитанных для двух периодов по одной и той же фиксированной структуре весов (на уровне отчетного или базисного периода).

По аналогии можно показать динамику среднего показателя лишь за счет изменения только весов f при фиксировании индексируемой величины x. Такой индекс условно назван индексом структурных сдвигов, который определеятся при фиксировании индексируемой величины на уровне базисного периода x ₀ по самой распространенной[58] формуле (204):

, (204)

Формулы (203) – (204) обычно применяются в тех случаях, когда влияние изменения структуры совокупности на динамику среднего показателя сильнее (1-ый фактор) влияния изменения только самой индексируемой величины (2-ой фактор)[59].

Если от абсолютных весов f перейти к относительным весам (долям) по формуле (6), то формулы (202) – (204) примут следующий вид:

; (205) ; (206) . (207)

В формулах (202) – (207) при анализе конкретных качественных индексируемых показателей (например, цены товара, себестоимости, производительности труда, урожайности и т.п.) вместо обозначений x и f должны использоваться другие общепринятые обозначения.

Например, при анализе такого качественного показателя как цена формулы (202) – (207) примут следующий вид:

; (208)

; (209) . (210)

Нетрудно заметить, что индекс переменного состава есть произведение индекса фиксированного состава на индекс структурных сдвигов:

. (211)

Из формулы (211) видно, что, например, индекс структурных сдвигов можно рассчитать путем деления индекса переменного состава на индекс фиксированного состава.

В нашем примере про дедушку определяем индекс переменного состава по формуле (208):

, то есть средняя цена яблок сегодня составляет 99,06% от вчерашней, то есть средняя цена снизилась с 21,2 руб. до 21,0 руб. за кг, что составило 0,94%.

Чтобы исключить влияние изменения структуры продаж яблок на динамику средней цены, рассчитаем индекс цены фиксированного состава по формуле (209)[60]:

.

Влияние изменения структуры продаж (доля продаж яблок сорта «антоновка» увеличилась, а сорта «белый налив» – уменьшилась) на динамику средней цены яблок отразим с помощью индекса структурных сдвигов, расчитав его по формуле (210):

=0,9838.

Проверку правильности расчетов выполним по формуле (211): 1,0069*0,9838 = 0,9906.

Поиск по сайту: