АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

V. Для дискретної випадкової величини Х, заданої рядом розподілу, знайти:

Читайте также:
  1. АКУСТИЧНІ ВЕЛИЧИНИ
  2. Алекс спустился со сцены и уселся на неё рядом с девочкой.
  3. Величини
  4. Визначення величини резерва сумнівних боргів на основі класифікації дебіторської заборгованості
  5. Вимірювані величини і методи вимірювань
  6. Випадкові величини та їх розподіл
  7. Випадкові події і величини, їх числові характеристики
  8. Відносні статистичні величини, їх види за аналітичною функцією, економічний зміст, методика обчислення та одиниці вимірювання
  9. Вплив величини напруги і параметрів ланцюга на перехідний процес
  10. Дискретні випадкові величини
  11. Дискретні випадкові величини і їх числові характеристики

а) ;

б) інтегральну функцію розподілу, побудувати її графік;

в) математичне сподівання, дисперсію, середнє квадратичне відхилення.

1.             2.        
0,2 0,1 0,3 0,1   0,2 0,3 0,1

 

3. –2           4.        
0,3 0,2 0,1 0,2   0,1 0,2 0,3

 

 

5. –3 –1         6. –1      
0,1 0,3 0,2 0,1   0,3 0,2 0,4

 

7.             8. –3      
0,1 0,3 0,1 0,2   0,1 0,2 0,1

 

9.             10.        
0,2 0,3 0,1 0,1   0,2 0,1 0,3

 

11. –2 –1         12.        
0,3 0,2 0,1 0,3   0,3 0,4 0,1

 

13.             14.        
0,1 0,3 0,1 0,2   0,1 0,5 0,1

 

15.             16. –4 –2    
0,3 0,2 0,1 0,1   0,1 0,2 0,2

 

17. –1           18.        
0,1 0,2 0,2 0,3   0,4 0,1 0,1

 

19. –5 –3         20.        
0,3 0,1 0,3 0,1   0,3 0,4 0,1

 

21.             22.        
0,2 0,2 0,1 0,1   0,1 0,3 0,3

 

23. –6           24.        
0,1 0,2 0,3 0,3   0,6 0,1 0,1

 

25. –4 –2         26.        
0,5 0,1 0,1 0,2   0,4 0,2 0,1

 

27.         11   28. –1      
0,2 0,2 0,1 0,3   0,5 0,1 0,3

 

29. –4           30.        
0,1 0,1 0,3 0,2   0,1 0,2 0,5

 

VI. Неперервна випадкова величина Х задана інтегральною функцією

розподілу. Знайти:

а) диференціальну функцію 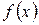(густину розподілу ймовірності);

б) ймовірність попадання випадкової величини в інтервал ;

в) математичне сподівання і дисперсію;

г) побудувати графіки , .

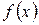1.   2.  

 

 

  3.   4.  
 
  5.   6.  
 
  7.   8.  
 
9.   10.    
 
11.   12.    
 
13.   14.    
 
             

 

 

15.   16.  
17.   18.  
19.   20.  
21.   22.  
23.   24.  
25.   26.  

 

 

27.   28.  
29.   30.  

VII. За спостереженнями над ознакою Х складений статистичний розподіл вибірки. Побудувати полігон відносних частот і кумулятивну криву. Знайти емпіричну функцію і побудувати її графік. Обчислити вибіркову середню, дисперсію і середнє квадратичне відхилення.

1.             2.          
                     

 

3.             4.          
                     
5.             6.          
                     

 

7.             8.          
                     
9.             10.          
                     
11.             12.          
                     
13.             14.          
                     
15.             16.          
                     
17.             18.          
                     

 

19.             20.          
                     
21.             22.          
                     

 

23.             24.          
                     
25.             26.          
                     
27.             28.          
                     
29.             30.          
                     

VIII. У припущенні про нормальний розподіл ознаки знайти теоретичні частоти за допомогою інтегральної функції розподілу і густини ймовірності. Перевірити на основі критеріїв Пірсона, Колмогорова, Романовського погодженість фактичних і теоретичних частот

1.

1-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14
                         

 

2.

2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14 14-15
                         

 

3.

3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14 14-15 15-16
                         

 

4.

4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14 14-15 15-16 16-17
                         

 

5.

5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14 14-15 15-16 16-17 17-18
                         

 

6.

6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14 14-15 15-16 16-17 17-18 18-19
                         

 

7.

7-8 8-9 9-10 10-11 11-12 12-13 13-14 14-15 15-16 16-17 17-18 18-19 19-20
                         

8.

8-9 9-10 10-11 11-12 12-13 13-14 14-15 15-16 16-17 17-18 18-19 19-20 20-21
                         

 

9.

9-10 10-11 11-12 12-13 13-14 14-15 15-16 16-17 17-18 18-19 19-20 20-21 21-22
                         

 

10.

10-11 11-12 12-13 13-14 14-15 15-16 16-17 17-18 18-19 19-20 20-21 21-22 22-23
                         

 

11.

1-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14
                         

12.

2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14 14-15
                         

 

13.

3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14 14-15 15-16
                         

 

14.

4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14 14-15 15-16 16-17
                         

 

15.

5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14 14-15 15-16 16-17 17-18
                         

 

16.

6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14 14-15 15-16 16-17 17-18 18-19
                         

 

17.

7-8 8-9 9-10 10-11 11-12 12-13 13-14 14-15 15-16 16-17 17-18 18-19 19-20
                         

 

 

18.

8-9 9-10 10-11 11-12 12-13 13-14 14-15 15-16 16-17 17-18 18-19 19-20 20-21
                         

 

19.

9-10 10-11 11-12 12-13 13-14 14-15 15-16 16-17 17-18 18-19 19-20 20-21 21-22
                         

 

20.

10-11 11-12 12-13 13-14 14-15 15-16 16-17 17-18 18-19 19-20 20-21 21-22 22-23
                         

 

21.

1-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14
                         

22.

1-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14
                         

 

23.

1-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14
                         

 

24.

1-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14
                         

 

25.

1-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14
                         

 

26.

1-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14
                         

 

27.

1-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14
                         

 

 

28.

1-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14
                         

 

29.

1-2 2-3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10-11 11-12 12-13 13-14
                         

 

30.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.031 сек.)