АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

IV. ПОВТОРНІ ВИПРОБУВАННЯ

Читайте также:
  1. Завдання та способи випробування перспективних горизонтів
  2. Задачі на використання формул при повторних випробуваннях
  3. Ймовірність відхилення відносної частоти від сталої ймовірності в незалежних випробуваннях
  4. Лекція 3. ПОСЛІДОВНІ НЕЗАЛЕЖНІ ВИПРОБУВАННЯ
  5. Лекція 41: Повторні незалежні випробування. Формула Бернуллі. Статистичне визначення ймовірності.
  6. Принципова схема і основи технології випробування пласта пластовипробувачем
  7. Припустимо, що у результаті випробування отримано інтервальний варіаційний ряд ознаки
  8. Формули Бейеса дозволяють переоцінювати ймовірності гіпотез після того, як становиться відомим результат випробування, в якому з’являється подія А.

 

Схема Бернуллі – послідовність випробувань, що задовольняють умовам:

ü число випробувань фіксоване,

ü кожне з випробувань приводить до одного з двох взаємовиключних наслідків,

ü ймовірності цих наслідків постійні у всіх випробуваннях,

ü випробування незалежні.

Нехай проведено незалежних випробувань, у кожному з яких подія може з’явитися з постійною ймовірністю . Ймовірність ненастання події в кожному випробуванні дорівнює : 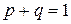. Потрібно обчислити ймовірність того, що в незалежних випробуваннях подія з’явиться рівно раз: .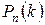

Формула Бернуллі

Якщо ймовірність появи події в кожному випробуванні постійна, а число випробувань невелике , то ймовірність того, що подія при незалежних випробуваннях з’явитися рівно раз, можна визначити за формулою:

.

Ймовірність того, що подія наступить


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.007 сек.)