Лекція 41: Повторні незалежні випробування. Формула Бернуллі. Статистичне визначення ймовірності

План.

1.Статистичне визначення імовірності.

2.Повторні незалежні випробування. Формула Бернуллі.

Статистичне визначення імовірності.

Розглянемо випадковий експеримент, що полягає в тім, що підкидається гральна кістка, зроблена з неоднорідного матеріалу. Її центр ваги не перебуває в геометричному центрі. У цьому випадку ми не можемо вважати результати (випадання одиниці, двійки й т.д.) рівноймовірними. З фізики відомо, що кістка більш часто буде падати на ту грань, що ближче до центра ваги. Як визначити ймовірність випадання, наприклад, трьох очка? Єдине, що можна зробити, це підкинути цю кістку n раз (де n-досить велике число, скажемо n =1000 або n =5000), підрахувати число випадань трьох очка n₃ і вважати ймовірність результату, що полягає у випаданні трьох очка, рівної n₃ / n – відносній частоті випадання трьох очка. Аналогічним образом можна визначити ймовірності інших елементарних результатів – одиниці, двійки, четвірки й т.д. Теоретично такий образ дій можна виправдати, якщо ввести статистичне визначення ймовірності.

Імовірність P( w _i) визначається як межа відносної частоти появи результату w _i у процесі необмеженого збільшення числа випадкових експериментів n, тобто

,

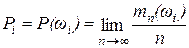де m_n (w _i) – число випадкових експериментів (із загального числа n зроблених випадкових експериментів), у яких зареєстрована поява елементарного результату w_i.

Тому що тут не приводиться ніяких доказів, ми можемо тільки сподіватися, що межа в останній формулі існує, обґрунтовуючи надію життєвим досвідом й інтуїцією.

У практиці дуже часто виникають задачі, у яких який-небудь інший спосіб визначення ймовірності події, крім статистичного визначення, знайти неможливо або вкрай важко.

Повторні незалежні випробування. Формула Бернуллі.

Розглянемо випадок багаторазового повторення того самого випробування або випадкового експерименту. Результат кожного випробування будемо вважати не залежним від того, який результат наступив у попередніх випробуваннях. Як результати або елементарних результатів кожного окремого випробування будемо розрізняти лише дві можливості: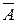

1) поява деякої події А;

2) поява події 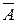, (події, що є доповненням А)

Нехай імовірність P (A) появи події А постійна й дорівнює p ( 0<. p <1). Імовірність P (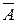) події 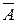позначимо через q: P (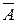) = 1– p=q.

Прикладами таких випробувань можуть бути:

1) підкидання монети: А – випадання герба; 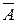– випадання цифри.

P (A) = P (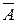) = 0,5.

2) кидання гральної кістки: А – випадання кількості очок, рівного п'яти, 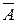випадання будь-якої кількості очок крім п'яти.

P (A) =1/6, P (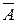) =5/6.

3) добування навмання з урни, що містить 7 білих й 3 чорних кулі, однієї кулі (з поверненням): А – добування білої кулі, 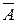– добування чорної кулі

P (A) = 0,7; P (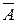) = 0,3

Нехай зроблено n випробувань, які ми будемо розглядати як один складний випадковий експеримент. Складемо таблицю з n кліток, розташованих у ряд, пронумеруємо клітки, і результат кожного випробування будемо відзначати так: якщо в i-м випробуванні подія А відбулося, то в i-ю клітку ставимо цифру 1, якщо подія А не відбулося (відбулася подія 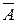), в i-ю клітку ставимо 0.

Якщо, наприклад, проведено 5 випробувань, і подія А відбулося лише в 2 -м й 5-м випробуваннях, то результат можна записати такою послідовністю нулів й одиниць: 0; 1; 0; 0; 1.

Кожному можливому результату n випробувань буде відповідати послідовність n цифр 1 або 0, що чергуються в тім порядку, у якому з'являються події A й 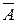в n випробуваннях, наприклад:

1; 1; 0; 1; 0; 1; 0; 0;... 0; 1; 1; 0

n цифр

Усього таких послідовностей можна скласти 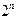(це читач може довести сам).

Тому що випробування незалежні, то ймовірність P кожного такого результату визначається шляхом перемножування ймовірностей подій A й 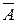у відповідних випробуваннях. Так, наприклад, для написаного вище результату знайдемо

P = p×p×q×p×q×p×q×q×...×q×p×p×q

Якщо в написаній нами послідовності одиниця зустрічається х раз (це значить, що нуль зустрічається n – x раз), то ймовірність відповідного результату буде pⁿq^n-x незалежно від того, у якому порядку чергуються ці x одиниць й n–x нулів.

Всі події, що полягають у тім, що в n випробуваннях подія A відбулося x раз, а подія 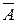відбулася n-x раз, є неспільними. Тому для обчислення ймовірності об'єднання цих подій (або суми цих подій), потрібно скласти ймовірності всіх цих подій, кожна з яких дорівнює pⁿq^n-x . Усього таких подій можна нарахувати стільки, скільки можна утворити різних послідовностей довжини n, що містять x цифр "1" й n–x цифр "0". Таких послідовностей виходить стільки, скількома способами можна розмістити x цифр "1" (або n – x цифр "0") на n місцях, тобто число цих послідовностей дорівнює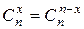

Звідси виходить формула Бернуллі:

P_n (x) =

По формулі Бернуллі розраховується ймовірність появи події A " x " раз в n повторних незалежних випробуваннях, де p – імовірність появи події A в одному випробуванні, q - імовірність появи події 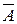в одному випробуванні.

Сформульовані умови проведення випробувань іноді називаються " схемою повторних незалежних випробувань " або " схемою Бернуллі "

Число x появи події A в n повторних незалежних випробуваннях називається частотою.

Приклад. З урни, що містить 2 білих й 6 чорних куль, навмання вибирається з поверненням 5 разів підряд одна куля. Підрахувати ймовірність того, що 4 рази з'явиться біла куля.

У наведені вище позначеннях n =8; p =1/4; q =3/4; x =5. Шукану ймовірність обчислюємо по формулі Бернуллі:

По формулі Бернуллі можна підрахувати ймовірності всіх можливих частот: x =0,1,2,3,4,5.

Помітимо, що якщо в цій задачі вважати, що білих куль було 20000, а чорних 60000, те очевидно p й q залишаться незмінними. Однак у цій ситуації можна зневажити поверненням витягнутої кулі після кожної вибірки (при не занадто більших значеннях x) і вважати ймовірності всіх частот: x =0,1,2,... по формулі Бернуллі.

Формула Бернуллі при заданих числах p й n дозволяє розраховувати ймовірність будь-якої частоти x (0 £ x £ n). Виникає природне запитання, якій частоті буде відповідати найбільша ймовірність?

Припустимо, що така частота існує, і спробуємо неї визначити з умови, що ймовірність цієї частоти не менше ймовірності "попередньої" й "наступної" частот:

P_n (x) ³ P_n (x – 1); P_n (x) ³ P_n (x+ 1) (*)

Перша нерівність (*) представляється у вигляді:

,

що еквівалентн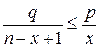о або 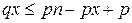. Звідси треба:

Вирішуючи другу нерівність (1), одержимо

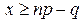
Таким чином, частота, що має найбільшу ймовірність (наймовірніша частота), визначається подвійною нерівністю

Якщо np + p – ціле число (тоді й np – q – ціле число), то дві частоти: x=np – q й x=np + p мають найбільшу ймовірність.

Лекція 42: Формула повної ймовірності.

Нехай деяка подія А може відбутися разом з одним з несумісних подій , що становлять повну групу подій. Нехай відомі ймовірності цих подій 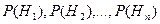й умовні ймовірності настання події А при настанні події H_i .

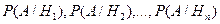Теорема. Імовірність події А, що може відбутися разом з одним з подій , дорівнює сумі парних добутків ймовірностей кожного із цих подій на відповідні їм умовні ймовірності настання події А.

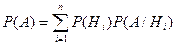
Фактично ця формула повної ймовірності вже використалася при рішенні прикладів, наведених вище, наприклад, у задачі з револьвером.

Доказ.

Т. к. події утворять повну групу подій, то подія А можна представити у вигляді наступної суми:

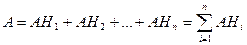
Т. к. події несумісні, те й події AH_i теж несумісні. Тоді можна застосувати теорему про додавання ймовірностей несумісних подій:

При цьому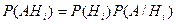

Остаточно одержуємо: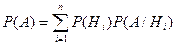

Теорема доведена.

Формула Байеса. Якщо Н_1, Н₂ , …, Н_n - повна група подій Р(Н_і)>0 (i= 1, 2, …, n), а В - довільна випадкова подія (В Î Á), така, що Р(В)>0, то

.

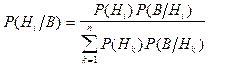Апріорні та апостеріорні ймовірності. Нехай подія А може проходити в різних умовах, про характер яких можна зробити n гіпотез Н₁, Н₂, …, Н_n. Із якихось міркувань відомі ймовірності цих гіпотезР(Н ₁), Р(Н₂), …, Р(Н_n) (апріорні ймовірності), відомі також умовні ймовірності Р(А /Н ₁), Р(А /Н₂), …, Р(А /Н_n). Припустимо, що в результаті проведення досліду наступила подія А. Це повинно визвати переоцінку ймовірностей

гіпотез Н_і; формули Байєса і дають вираз для умовних ймовірностей Р(Н_i/А) (ці ймовірності називають апостеріорними ймовірностями).

Задача 1. В урну, яка містить дві кулі, покладена біла куля, після чого з неї навмання вилучена одна куля. Найти ймовірність того, що вилучена куля буде білою, якщо рівноможливі всі можливі припущення щодо початкового складу білих куль. Розв’язування. Нехай подія А – вилучена біла куля. Можливі наступні припущення (гіпотези) про початковий склад куль: Н₁ – білих куль немає. Н₂ – одна біла куля. Н₃ – дві білі кулі. Оскільки є всього три гіпотези, причому за умовою задачі вони рівноможливі, і сума ймовірностей гіпотез дорівнює одиниці (оскільки вони утворюють повну групу подій), то ймовірність кожної з гіпотез дорівнює 1/3, тобто Р(Н₁) =Р(Н₂)= Р(Н₃)=1/3.
Умовна ймовірність того, що буде вилучена біла куля, при умові, що спочатку в урні не було білих куль, Р (А/H₁)= 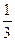. Умовна ймовірність того, що буде вилучена біла куля, при умові, що спочатку в урні була 1 біла куля, Р (А/H₂)= . Умовна ймовірність того, що буде вилучена біла куля, при умові, що спочатку в урні було 2 білі кулі, Р (А/H₃)= 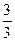=1. Шукану ймовірність того, що буде вилучена біла куля, знаходимо за формулою повної ймовірності

Р(А) = Р(А/Н₁) Р(Н₁) + Р(А/Н₂) Р(Н₂) +Р(А/Н₃) Р(Н₃) = 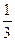. 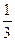+ 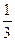. + 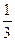.1= .

Лекція 42: Закон великих чисел.

Визначення. Говорять, що послідовність випадкових величин 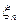, по ймовірності збігається до випадкової величини 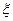, якщо для довільного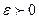

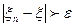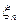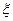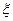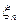Р { }=0. Збіжність по ймовірності послідовності до позначають так: ₌plim , або _.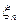

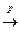
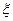Нехай 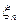послідовність випадкових величин, для яких існують М 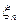. Законом великих чисел називають теореми, які стверджують, що різниця

збігається до нуля по ймовірності.

Задача. Довести, коли існує M 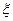² i М =а, то 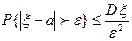(нерівність Чебишова).

Теорема Чебишова. Нехай { 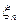}- послідовність незалежних випадкових величин, існують 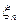D i D 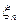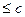при всіх n. Тоді

. (*)

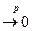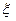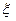Наслідок. Нехай ₁, ₂,…, 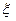_n,…- послідовність незалежних випадкових величин така, що М 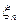=а, D 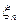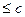, n=1,2,…

Тоді для кожного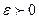

.

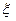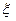Цей частковий випадок теореми Чебишова дає обґрунтування правилу середнього арифметичного в теорії обробки результатів вимірювання. Припустимо, що необхідно виміряти деяку фізичну величину а. Повторюючи вимірювання n раз в однакових умовах, спостерігач одержує результати вимірювань ₁, ₂,…, 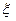_n [1]. Якщо спостереження не мають систематичної помилки, тобто М 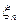=а, то згідно сформульованому вище наслідку,

Теорема Хінчина. Нехай { 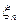}- послідовність незалежних однаково розподілених величин, які мають скінчене математичне сподівання М 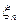=а. Тоді для кожного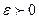

.

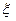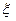Теорема Маркова. Нехай випадкові величини ₁, ₂,…, 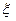_n як завгодно залежні. Для виконання (*) достатньо, щоб

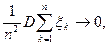при .

Теорема Бернуллі. Нехай маємо послідовність випробовувань, в кожному з яких можуть бути два наслідки - успіх У (з ймовірністю р) або невдача Н (з ймовірністю q=1-p) незалежно від наслідків інших випробувань. Утворимо послідовність випадкових величин наступним чином. Нехай 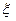_к =1, якщо в к-тому випробовуванні був успіх 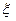_к =0, якщо в к-тому випробовуванні наступила невдача. Тоді { 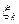}- є послідовність незалежних однаково розподілених випадкових величин M 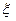_к=p, D 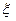_к=pq. Випадкова величина 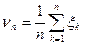представляє собою частоту появи успіху в перших n випробуваннях. Оскільки для послідовності { 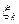} - виконані умови теореми Чебишова, то із теореми Чебишова одержуємо наступне твердження.

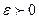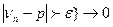Теорема Бернуллі. Для довільного Р{ при n .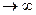

Зміст цього твердження полягає в тому, що ведене нами визначення ймовірності відповідає інтуїтивному розумінню ймовірності як границі частоти.

Посилений закон великих чисел.

Послідовність випадкових величин { 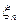,n }- збігається з ймовірністю 1 до величини 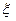, якщо ймовірність всіх тих точок 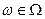, для яких 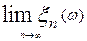не існує,

або 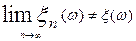, дорівнює нулю, тобто якщо Р{{ .

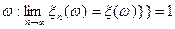Розглянемо послідовність випадкових величин 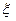_k з скінченими математичними сподіваннями. Теореми, які стверджують, що різниця збігається з ймовірністю 1 до нуля, називається посиленим законом великих чисел. Нижче приводиться дві теореми про посилений закон великих чисел, обидві вони доведені.

А. М. Колмагоровим.

Теорема 1. Нехай 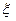_n – послідовність незалежних випадкових величин, для яких М 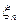, D 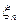визначені. Якщо

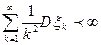, то Р {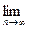 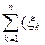- )=0}=1.

Наслідок (теорема Бореля). Припустимо, що розглядається послідовність незалежних випробувань, в кожному з яких з’являється успіх У з ймовірністю р або невдача Н з ймовірністю q=1-p. Нехай - число успіхів при n випробуваннях. Тоді Р{ 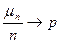}=1.

Це випливає з того, що 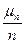= , де 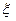_k- послідовність незалежних випадкових величин введених при доведенні теореми Бернуллі.

Теорема 2. Нехай 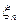- послідовність незалежних однаково розподілених величин з скінченим математичним сподіванням М 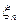=а. Тоді

Р { 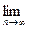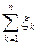=а}=1.

Центральна гранична теорема.

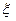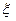Теорема. Нехай ₁, ₂,…, 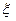_n,…- послідовність незалежних випадкових величин з скінченною дисперсією ( і

.

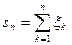Тоді при n 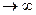для довільного x

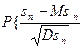
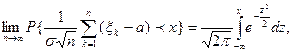( де = )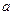

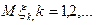Лекція 43: Поняття про статистику та її методи. Статистичні таблиці.

План.

1.Статистика та її методи.

2.Набір експериментальних даних.

3.Вибірка.

4.Наочне представлення статистичного матеріалу.

5.Точковий та інтервальний розподіл частот.

6.Полігон та гістограма.

7.Мода і медіана.

Статистика- наука, що збирає, обробляє і вивчає різні дані, пов’язані з масовими явищами, процесами, подіями. Предметом вивчення статистики є кількісна сторона цих явищ. Статистика вчить, як проаналізувати інформацію, виявити та оцінити закономірності формування, розвитку, взаємодії цих складних за своєю природою соціально-економічних явищ.

Математична статистика – розділ математики, присвячений математичним методам систематизації, обробки, дослідження статистичних даних для наукових іпрактичних висновків. ЇЇ широко застосовують: астрономія (розподіл зірок на небі), фізика (термодинаміка), біологія (закони спадковості), гідрологія (прогноз погоди), індустрія (контроль якості знань).

Статистика виникла з потреб людини, необхідності обліку земельних угідь, кількості населення, вікового складу та ін. В Англії Х\/ІІ ст. людей, що займалися цими питаннями називали «політичними арифметиками».

Математична статистика виникла у Х\/ІІ ст.. і створювалась паралельно з теорією ймовірностей. Дальший розвиток статистика одержала в працях

П.Л.Чебишова, А.А.Маркова, О.М.Ляпунова, К.Гауса, К.Пірсона. В ХХст. суттєвий вклад у розвиток статистики внесли А.М Колмогоров, М.В.Смирнов, Стьюдент, Ф.Фішер, Е.Пірсон.

Першим етапом дослідження є статистичне спостереження.

Спостереження – це спланований, науково-організований збір масових даних про соціально-економічні явища та процеси. Наприклад: облік відвідування, облік успішності.

Види статистичних спостережень:

1) за часовою ознакою (поточні, періодичні, одиночні),

2) за способом організації (звітні, експедиційні, само обчислення),

3) за ступенем повноти охоплення одиниць(суцільні і несуцільні-вибіркові, спостереження основного масиву, анкетні, монографічні).

Найпоширеніше спостереження – вибіркове. В процесі вибіркового спостереження вивчається лише частина сукупності, відібрана певним чином, яка називається вибіркою. Всю сукупність, з якої роблять вибірку, називають генеральною сукупністю. Число об’єктів генеральної сукупності чи вибірки називають обсягом (об’ємом) генеральної сукупності чи вибірки.

Матеріал спостережень подають у таблицях.

Статистичні таблиці мають підмет і присудок. Підмет- перелік об’єктів або груп їх. Присудок – це ознаки або показники, що характеризують підмет.

Таблиці бувають: прості, групові, комбінаційні.

Замість слова «дані» використовують термін «варіанти». Числова характеристика варіанти називається ознакою. варіанти записані в таблиці за зростанням чи спаданням, називають варіаційним рядом. вибіркові ряди бувають дискретними та інтервальними.

Нехай вибіркові дані містять m варіант х₁, х₂, … х_m. Ознака Х прийняла значення х₁ всього n₁ раз, х₂ всього n₂ раз… Додатне число, що вказує, скільки разів та чи інша варіанта зустрічається, називається частотою.

Числа спостережень називають частотами: n₁, n₂, …n_m, а їх відношення до обсягу вибірки 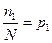, … 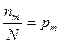- відносними частотами.

Сума відносних частот дорівнює 1.

Статистичним рядом розподілу вибірки називається перелік варіант і відповідних їм частот.

Наприклад:

Для графічного зображення статистичного розподілу використовуються полігони і гістограми.

Вибірка характеризується центральними тенденціями: середнім значенням, модою, медіаною.

Середнє значення- середнє арифметичне всіх її значень.

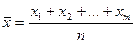або .

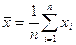Мода вибірки – значення, що зустрічається найчастіше, М₀.

Медіана вибірки – число, що поділяє навпіл упорядковану сукупність вибірки, М_е.

Наприклад: для вибірки 2;3;4;4;6;6;6;7;7;8 середнє арифметичне 5,3; мода6 і медіана 6.

Різниця виду 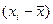називається відхиленням.

Середнє квадратичне відхилення знаходять так:

-усі відхилення підносять до квадрата;

-знаходять середнє арифметичне цих квадратів;

-із одержаного числа добувають квадратний корінь.

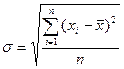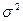. - дисперсія.

Поиск по сайту: