АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Геометричний зміст похідної. Рівняння дотичної

Читайте также:
  1. V. Зміст теми заняття.
  2. Бухгалтерський баланс,його побудова, зміст і оцінка статей.
  3. Бюджетні обмеження споживача, бюджетне рівняння та фактори впливу на бюджетну лінію.
  4. В) становлять зміст соціального захисту безробітних.
  5. Взаємозв'язок етапів аналізу з метою і змістом робіт
  6. Визначити зміст «соціології молоді» – 15 б.
  7. Визначте зміст соціального конфлікту – 15 б.
  8. Визначте зміст соціології молоді – 15 б.
  9. Вимоги до змісту загальної середньої освіти
  10. Вимоги до змісту та розташування реквізитів
  11. Вимоги щодо змісту та оформлення документів
  12. Відносні статистичні величини, їх види за аналітичною функцією, економічний зміст, методика обчислення та одиниці вимірювання

Кутовий коефіцієнт дотичної до прямої y=f(x) в точці Мо(хо; уо) або тангенс кута α, що утворює дотична до прямої в даній точці з додатнім напрямом осі ОХ, – це похідна f ′(x0) в даній точці: k=tgα=f ′(x0). Це геометричний зміст похідної.

У точці М(х0;у0) проведемо дотичну до кривої 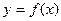. Складемо рівняння дотичної, знаючи координати точки дотику і рівняння кривої. Дотична – це пряма . Знайдемо 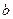, скориставшись що, дотична проходить через точку М(х0;у0). , яке підставимо у рівняння дотичної і одержимо .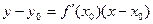

- рівняння дотичної до кривої 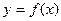в точці М(х0;у0).

План складання дотичної до кривої:

1) Знайти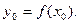

2) Знаходимо .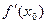

3) Робимо підстановку даних у рівняння дотичної.

Лекція 26.

Тема: Похідні елементарних функцій. Похідні суми, добутку і частки функцій.

План.

1.Похідна сталої функції.

2.Похідна степеневої функції з цілим показником.

3.Похідні тригонометричних функцій.

4.Правила обчислення похідних.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)