Відносні статистичні величини, їх види за аналітичною функцією, економічний зміст, методика обчислення та одиниці вимірювання

Відносний показник - показник у формі відносної величини - це результат порівняння одного абсолютного показника з іншим; характеризує співвідношення між кількісними характеристиками процесів і явищ, що вивчаються, чи міру кількісного співвідношення різнойменних чи однойменних показників.

При розрахунках відносних величин порівнювана величина - це величина, що знаходиться в чисельнику дробу; база порівняння - це величина, що знаходиться у знаменнику дробу, тобто це показник, з яким проводиться порівняння. Якщо при розрахунку структури в цілому ми не отримуємо 1 чи 100%, то необхідно здійснити коригування структури. При аналізі структури в динаміці використовується показник структурних зрушень у відсоткових пунктах. Відсотковий пункт визначається як різниця між часткою і -ї складової сукупності поточного року й відповідною часткою тієї самої складової минулого року. Слід зауважити, що при цьому структури явища за поточний і попередній роки мають бути порівнянними, тобто відображати однакову кількість складових в однакових межах.

Форми вираження відносних величин:

• коефіцієнт: база порівняння = 1 (точність розрахунку - 0,000);

• відсоток: база порівняння = 100 % (точність розрахунку - 0,0);

• проміле: база порівняння = 1000 (точність розрахунку - 0);

· відносні показники інтенсивності є іменованими величинами.

Використовують сім видів відносних величин, характеристика яких і методика обчислення наведені у таблиці 5.1.

Таблиця 5.1

Види відносних величин і порядок їх обчислення

Назва відносної величини	Що характеризує відносна величина	Методика обчислення	Розрахункова формула
1. Відносна величина планового завдання (прогнозування)	У скільки разів рівень плану (прогнозу) більший за рівень поточного періоду або яку частку становить від рівня поточного періоду	Рівень ознаки за планом на наступний період Фактичний рівень ознаки за базовий період	ВВПЗ = dПЗ =
Закінчення таблиці 5.1
2. Відносна величина виконання плану (договірних зобов’язань)	Рівень виконання плану, прогнозних розрахунків, договірних зобов’язань, державного замовлення	Фактичний рівень ознаки за звітний період Рівень ознаки за планом (прогнозом) за звітний період	ВВВП = dВП =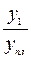
3. Відносна величина динаміки	Зміну явищ у часі	Рівень ознаки у поточному (звітному) періоді Рівень ознаки одного з попередніх періодів	ВВД = dД =
4. Відносна величина структури	Частку складових частин сукупності в їх загальному підсумку	Частина сукупності Уся сукупність	ВВС = dС =
5. Відносна величина координації	Співвідношення між складовими частинами однієї сукупності; показує у скільки разів одна частина сукупності більша за іншу частину цієї ж сукупності або яку частку одна частина сукупності становить від рівня іншої частини цієї ж сукупності	Відношення однієї зі складових частин сукупності до іншої частини сукупності, обраної за базу порівняння (база порівняння обирається довільно)	ВВК = dК =
6. Відносна величина просторового порівняння	Співвідношення однойменних показників різних сукупностей за один і той самий проміжок часу	Абсолютна велична ознаки одного об’єкта Абсолютна величина такої ж ознаки іншого об’єкта	ВВПП = dПП =
7. Відносна величина інтенсивності	Ступінь поширення або розвиток явища в певному середовищі; показує скільки одиниць однієї сукупності припадає на одиницю іншої	Абсолютна величина певного явища Розмір середовища	ВВІ = dІ =

5.4. Середні величини у статистиці, їх види, умови наукового застосування та особливості обчислення

Однією з узагальнюючих характеристик в аналізі суспільних явищ є середня величина. Статистичні середні відображують об'єктивну наявність певних умов, які проявляються в кожній одиниці досліджуваної сукупності. Середня узагальнює весь діапазон даних і є результатом абстрагування відмінностей, що притаманні одиницям сукупності. У ній нівелюються випадкові відхилення, властиві індивідуальним значенням ознаки, яка вивчається, а також відображаються загальні умови, що формують досліджувану сукупність.

Порівняти ж між собою окремі сукупності за якоюсь конкретною ознакою можна за середнім її значенням, визначеним для кожної сукупності. Це можливо тому, що в середній величині відображається те типове, що характерне для всієї сукупності.

Розраховуючи конкретну середню, завжди доцільно опиратись на її логічну формулу (математичне вираження середньої), яка є відношенням обсягу ознаки до обсягу сукупності. Критерій правильного вибору форми середньої величини - це запис логічної формули розрахунку.

Для кожної середньої є лише одне правильне співвідношення, для реалізації якого залежно від даних, що існують, можна використовувати різні форми середніх: середню арифметичну, середню гармонічну, середню квадратичну, середню геометричну за не згрупованими (просту) і за згрупованими даними (зважену).

Однак в усіх випадках, коли характер величини, за якою розраховується середня, передбачає наявність ваги, неможливо замість зважених формул середніх використовувати прості, тобто незважені, формули. Використання кожного виду середніх залежить від двох обставин, по-перше, від характеру індивідуальних значень ознаки (прямі, обернені, квадратичні, відносні). По-друге, від характеру алгебраїчного зв’язку між індивідуальними значеннями ознаки та її загальним обсягом (сума, добуток, степень, квадратичний корінь).