 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Показники варіації та формули для їх розрахунку
| Назва показника | Розрахункова формула за даними | |
| не згрупованими | згрупованими | |
| Середнє лінійне відхилення | 
| 
|
| Середнє квадратичне відхилення |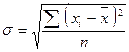 
| 
|
| Дисперсія | 
| 
|
хі – індивідуальні значення окремої ознаки, варіанти;
 – середня арифметична (середнє значення ознаки);
n – обсяг сукупності, кількість ознак у сукупності;
fi – частота відповідної ознаки.
|
Дисперсія являє собою середній квадрат відхилень, є відповідні властивості дисперсії і вона пов’язана з середнім квадратичним відхиленням таким співвідношенням:
,
де s – середнє квадратичне відхилення;
D = s 2 – дисперсія.
При порівнянні варіації різних ознак або однієї ознаки у різних сукупностях використовуються відносні характеристики: коефіцієнти варіації. До них належать:
· лінійний коефіцієнт варіації, який обчислюється за формулою:
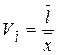, або 
·100 %,
де 
– середнє лінійне відхилення;
– середня арифметична;
· квадратичний коефіцієнт варіації, який обчислюється за формулою:
, або 
·100 %,
де s – середнє квадратичне відхилення;
· коефіцієнт осциляції, який обчислюється за формулою:
,
де R – розмах варіації.
Чим менше середнє відхилення, тим більш типова середня, тим більш однорідна сукупність. Найчастіше квадратичний коефіцієнт варіації використовують як критерій однорідності сукупності, він є ознакою надійності середньої.. У симетричному, близькому до нормального, розподілі Vσ = 0,33.
Для малих сукупностей розрізняють такі значення відносних коливань:
Vσ < 10% - незначне коливання, сукупність однорідна, значення середньої є типовим рівнем ознаки в даній сукупності;
10 % ≤ Vσ ≤ 33% - середнє коливання, сукупність в межах однорідності, значення середньої можна вважати типовим рівнем ознаки в даній сукупності;
Vσ > 33% - високий рівень варіації, сукупність неоднорідна, значення середньої неможна вважати типовим рівнем ознаки в даній сукупності.
Дисперсія альтернативної ознаки обчислюється як добуток часток за формулою:
,
де d 1 – частка елементів сукупності, яким властива ознака;
d 0 – частка решти елементів, у яких відсутня ознака (d 0 = 1 – d 1).
Дисперсія альтернативної ознаки широко використовується під час проектування вибіркових обстежень, обробці даних соціологічних опитувань, статистичному контролі якості продукції тощо.
Поиск по сайту: