 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Нескінченно великі функції і їх зв'язок з
1) За означенням логарифма.
а) б)
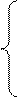
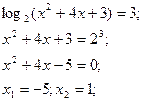
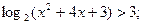
Перевірка: усно.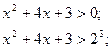 
Відповідь: -5; 1.
Відповідь: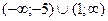 
.
2) Використання властивостей логарифмічної функції.
а) б)
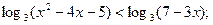
Перевірка: усно, 4-ст. корінь.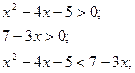 
Відповідь: -3. Відповідь: 
.
3) Введення нової змінної (підстановка)
а) б)
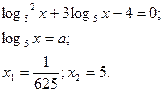
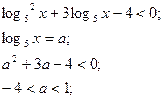
Відповідь: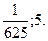 
Відповідь: 
.
4) Потенціювання.
а) б)
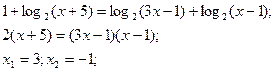
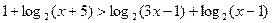
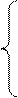
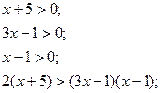
Перевірка: -1- ст..корінь.
Відповідь: 3. Відповідь: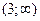 
.
5) Логарифмування.
а) б)
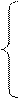
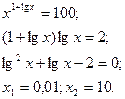
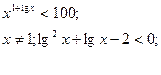
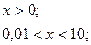
Відповідь: 0,01; 10. Відповідь: (0,01;10).
6) Зведення до одної основи.
а)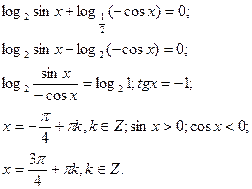 
Відповідь: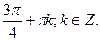 
б)
 |
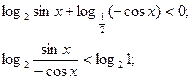
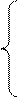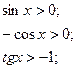
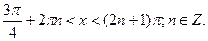
Відповідь: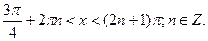
7) Використання основної логарифмічної тотожності.
а) б)
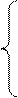
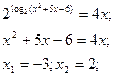
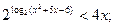
Перевірка: х=-3-ст. корінь.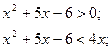 
Відповідь: 2.
Відповідь: (1;2).
Лекція 22.
Тема: Системи рівнянь з логарифмами.
Розв’язати системи рівнянь.
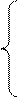
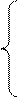1.
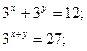
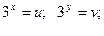
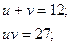
Відповідь: (1;2); (2;1).
2.
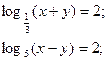
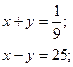
Відповідь: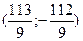 
.
3.№233(2) [№57(2)]; №232(2); [№56(2)].
Нескінченно великі функції і їх зв'язок з
нескінченно малими.
Означення. Межа функції f (x) при х®а, де а- число, рівний нескінченності, якщо для будь-якого числа М>0 існує таке число D>0, що нерівність
ïf (x)ï>M
виконується при всіх х, що задовольняють умові
0 < ïx - аï < D
Записується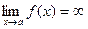 
.
Власне, якщо в приведеному вище визначенні замінити умову ïf (x)ï>M на f (x)>M, то одержимо:
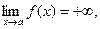
а якщо замінити на f (x)<M, то:
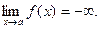
Графічно приведені вище випадки можна проілюструвати таким чином:
 |
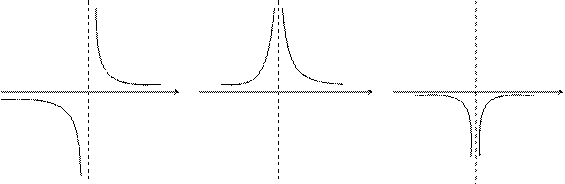а x а x а x
Означення. Функція називається нескінченно великою при х®а, де а – чослі або одна з величин ¥, +¥ або -¥, якщо 
, де А – число або одна з величин ¥, +¥ або -¥.
Зв'язок нескінченно великих і нескінченно малих функцій здійснюється відповідно до наступної теореми.
Теорема. Якщо f (x)®0 при х®а (якщо х®¥) і не звертається в нуль, то
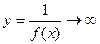
Лекція 24.
Тема: Неперервність функції.
Функція f(x) називається неперервною в точці х=а, якщо границя функції f(x) для х, що прямує до а, дорівнює значенню функції в точці а:
lim f(x)=f(а)
х 
а
План дослідження функції на неперервність в точці:
1) функція f(x) має бути визначена в деякому околі т. а; в т. а;
2) повинні існувати скінченні ліва границя
lim f(х)= f(а) і права lim f(x)=f(а)
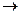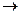х а-0 х а+0
3) lim f(х)= lim f(x)=f(а)
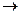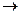х а-0 х а+0
Функція f(x) неперервна на всій області визначення, якщо неперервна в кожній її точці.
Розриви функцій:
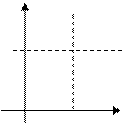
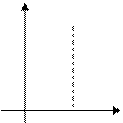
У У У У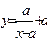 
у=f(x)
О хо Х хо Х хо Х О Х
f(xo-o)≠f(xo+o) f(xo-o)=f(xo+o)≠f(xo) lim f(x)= 
x 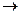a
розрив І роду розрив ІІ роду
Мал.46. Мал.47. Мал.48. Мал.49.
Наприклад:Дослідити на наявність розривів функцію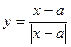 
Розв’язання.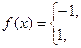 
.
Для х=а lim у=-1; lim у=1.
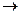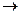x a-0 x a+0
Ліва і права границя існують, але не рівні – це розрив І роду.
Наприклад: Дослідити на наявність розривів функцію 
Розв’язання. При х=а f(x-a)=-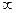 
; f(x+a)= 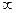границя не існує
– розрив ІІ роду.
Запитання для самоконтролю:
1) Які функції називають неперервними?
2) Який план дослідження функції на неперервність?
3) Що таке розрив І роду? А ІІ роду?
Властивості неперервних функцій:
1.Многочлен-функція неперервна на всій числовій осі, отже, такі функції, крім дробово-раціональних – неперервні.
2.Сума, різниця і добуток функцій є функція неперервна.
3.Дробово-раціональна функція неперервна в усіх точках, крім тих, що перетворюють знаменник на нуль.
4.Якщо функція – неперервна на проміжку, і на кінцях його приймає значення з різними знаками, то всередині проміжка знайдеться хоч одна точка, в якій дана функція перетворюється в нуль.
5.Якщо функція – неперервна на відрізку, то серед значень, що вона набуває на відрізку, існують найбільше і найменше значення. При цьому вона набуває значень між найбільшим і найменшим.
Лекція 25.
Тема: Задачі, які приводять до поняття похідної. Похідна. Механічний та геометричний зміст похідної.
План.
1.Задача про миттєву швидкість.
2.Задача про дотичну до кривої.
3.Поняття похідної.
4. Механічний зміст похідної.
5.Геометричний зміст похідної. Рівняння дотичної.
Поиск по сайту: