Перестановки з повторенням

Розглянемо множину, що містить однокові елементи типів. Скільки існує перестановок елементів першого типу, - другого типу,... - -го типу? Такі перестановки називаються перестановками з повторенням, їх кількість знаходять за формулою .

Наприклад: Скільки існує різних перестановок букв у слові “математика”?

Розв’язання:

Р(3а;2т;1е;2м;1и;1к)=

Лекція 38: Основні поняття теорії ймовірностей. Класичне означення ймовірності. Операції над подіями.

Розглянемо випадковий експеримент, що полягає в тім, що підкидається гральна кістка, зроблена з неоднорідного матеріалу. Її центр ваги не перебуває в геометричному центрі. У цьому випадку ми не можемо вважати результати (випадання одиниці, двійки й т.д.) рівноймовірними. З фізики відомо, що кістка більш часто буде падати на ту грань, що ближче до центра ваги. Як визначити ймовірність випадання, наприклад, трьох очка? Єдине, що можна зробити, це підкинути цю кістку n раз (де n-досить велике число, скажемо n =1000 або n =5000), підрахувати число випадань трьох очка n₃ і вважати ймовірність результату, що полягає у випаданні трьох очка, рівної n₃ / n – відносній частоті випадання трьох очка. Аналогічним образом можна визначити ймовірності інших елементарних результатів – одиниці, двійки, четвірки й т.д. Теоретично такий образ дій можна виправдати, якщо ввести статистичне визначення ймовірності.

Імовірність P( w _i) визначається як межа відносної частоти появи результату w _i у процесі необмеженого збільшення числа випадкових експериментів n, тобто

,

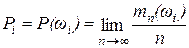де m_n (w _i) – число випадкових експериментів (із загального числа n зроблених випадкових експериментів), у яких зареєстрована поява елементарного результату w_i.

Тому що тут не приводиться ніяких доказів, ми можемо тільки сподіватися, що межа в останній формулі існує, обґрунтовуючи надію життєвим досвідом й інтуїцією.

У практиці дуже часто виникають задачі, у яких який-небудь інший спосіб визначення ймовірності події, крім статистичного визначення, знайти неможливо або вкрай важко.

Як уже говорилося раніше, множина елементарних результатів може бути більш, ніж рахунковим (тобто незліченним). Так незліченна множина результатів має експеримент, що складається у випадковому киданні крапки на відрізок [ a ₁; a ₂]. Можна собі представити, що експеримент, що полягає у вимірі температури в заданий момент у заданій крапці теж має незліченне число результатів (дійсно, температура може прийняти будь-яке значення з деякого проміжку, хоча в дійсності ми можемо вимірювати її лише з певною точністю, і практична реалізація такого експерименту дасть кінцеве число результатів). У випадку експерименту з нескінченною множиною елементарних результатів не можна вважати будь-яка підмножина множини подією. Варто помітити, що підмножини, що не є подіями, є математичними абстракціями й не зустрічаються в практичних задачах. Тому в нашому курсі даний параграф є необов'язковим.

Щоб ввести визначення випадкової події, розглянемо систему (кінцевих або рахункову) підмножин простору елементарних результатів.

У випадку виконання двох умов:

1) із приналежності А цій системі треба приналежність цій системі;

2) із приналежності й цій системі треба приналежність A_i A_j цій системі

така система підмножин називається алгеброю.

Нехай — деякий простір елементарних результатів. Переконаєтеся в тім, що дві системи підмножин:

1),; 2), А, 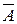, (тут А — підмножина W) є алгебрами.

Нехай A ₁ й A₂ належать деякій алгебрі. Доведіть, що A ₁ \ A₂ і належать цій алгебрі.

Назвемо s - алгеброю систему Á підмножин множини, що задовольняє умові 1) і умові 2)¢:

2) ¢ якщо підмножини А ₁, А ₂,¼, А_n, ¼належать Á, те їхнє рахункове об'єднання (за аналогією з підсумовуванням це рахункове об'єднання коротко записується формулою ) теж належить Á.

Підмножина А множини елементарних результатів є подією, якщо воно належить якійсь s - алгебрі.

Можна довести, що якщо вибрати будь-яку рахункову систему подій, що належать якоїсь (s-алгебрі й проводити із цими подіями будь-які прийняті в теорії множин операції (об'єднання, перетинання, узяття різниці й доповнення), те результатом буде множина або подія, що належить тієї ж (s-алгебрі.

Сформулюємо аксіому, називану аксіомою А.Н. Колмогорова.

Кожній події відповідає невід’ємне й не перевищуюче одиниці число P ( А ), назване ймовірністю події А, причому функція P ( А ) має наступні властивості:

1) Р ()= 1

2) якщо події A ₁, A ₂,..., A_n, ¼ несумісні, то

=

Якщо задано простір елементарних результатів, алгебра подій і визначена на ній функція Р, що задовольняє умовам наведеної аксіоми, то говорять, що задано імовірнісний простір.

Це визначення імовірнісного простору можна перенести на випадок кінцевого простору елементарних результатів. Тоді як алгебра можна взяти систему всіх підмножин множини.

Операції над подіями.

Визначення. Події А и В називаються рівними, якщо здійснення події А спричиняє здійснення події В и навпаки.

Визначення. Об'єднанням або сумою подій А_k називається подія A, що означає появу хоча б одного з подій А_k.

Визначення. Перетинанням або добутком подій A_k називається подія А, що полягає в здійсненні всіх подій A_k.

Визначення. Різницею подій А и В називається подія С, що означає, що відбувається подія А, але не відбувається подію В.

Визначення. Додатковою до події А називається подія , що означає, що подія А не відбувається.

Визначення. Елементарними результатами досліду називаються такі результати досліду, які взаємно виключають один одного й у результаті досліду відбувається одне із цих подій, також яке б не була подія А, по елементарному результаті, що наступив, можна судити про те, відбувається або не відбувається ця подія.

Сукупність всіх елементарних результатів досліду називається простором елементарних подій.

Визначення. Протилежними називаються дві несумісні події, що утворять повну групу.

Визначення. Подія А називається незалежною від події В, якщо імовірність появи події А не залежить від того, відбулася подія В чи ні. Подія А називається залежною від події В, якщо ймовірність появи події А міняється залежно від того, відбулася подія В чи ні.

Лекція 39: Імовірність суми подій.

Теорема (додавання ймовірностей). Імовірність суми двох несумісних подій дорівнює сумі ймовірностей цих подій.

Наслідок 1: Якщо події утворять повну групу несумісних подій, то сума їхніх ймовірностей дорівнює одиниці.

Визначення. Протилежними називаються дві несумісні події, що утворять повну групу.

Теорема. Імовірність появи хоча б одної із двох сумісних подій дорівнює сумі ймовірностей цих подій без імовірності їхньої спільної появи.

Наслідок 2: Сума ймовірностей протилежних подій дорівнює одиниці.

Лекція 40: Умовна ймовірність та незалежність подій. Імовірність добутку незалежних подій. Використання формул комбінаторики для обчислення імовірностей.

Визначення. Подія А називається незалежною від події В, якщо імовірність появи події А не залежить від того, відбулася подія В чи ні. Подія А називається залежною від події В, якщо ймовірність появи події А міняється залежно від того, відбулася подія В чи ні.

Визначення. Імовірність події В, обчислена за умови, що мала місце подія А, називається умовною ймовірністю події В.

Теорема. (Множення ймовірностей) Імовірність добутку двох подій (спільної появи цих подій) дорівнює добутку ймовірності одного з них на умовну ймовірність іншого, обчислену за умови, що перша подія вже наступила.

Також можна записати:

Доказ цієї теореми безпосередньо випливає з визначення умовної ймовірності.

Якщо події незалежні, то , і теорема множення ймовірностей приймає вид:

У випадку добутку декількох залежних подій імовірність дорівнює добутку одного з них на умовні ймовірності всіх інших за умови, що ймовірність кожного наступного обчислюється в припущенні, що всі інші події вже відбулися.

З теореми добутку ймовірностей можна зробити висновок про ймовірності появи хоча б однієї події.

Якщо в результаті випробування може з'явитися п подій, незалежних у сукупності, то ймовірність появи хоча б одного з них дорівнює

Тут подія А означає настання хоча б одної з подій A_i, а q_i – імовірність протилежних подій .

Приклад. У барабані револьвера перебувають 4 патрона із шести в довільному порядку. Барабан розкручують, після чого натискають на спусковий гачок два рази. Знайти ймовірності хоча б одного пострілу, двох пострілів, двох осічок.

Імовірність пострілу при першому натисканні на курок (подія А) дорівнює , імовірність осічки - Імовірність пострілу при другому натисканні на курок залежить від результату першого натискання.

Так якщо в першому випадку відбувся постріл, то в барабані залишилося тільки 3 патрона, причому вони розподілені по 5 гніздам, тому що при другому натисканні на курок напроти стовбура не може виявитися гніздо, у якому був патрон при першому натисканні на курок.

Умовна ймовірність пострілу при другій спробі - якщо в перший раз був постріл, - якщо в перший раз відбулася осічка.

Умовна ймовірність осічки в другий раз - , якщо в перший раз відбувся постріл, - якщо в перший раз була осічка.

Розглянемо ймовірності того, що в другому випадку відбудеться постріл (подія В) або відбудеться осічка (подія ) за умови, що в першому випадку відбувся постріл (подія А) або осічка (подія ).

- два постріли підряд

- перша осічка, другий постріл

- перший постріл, друга осічка

- дві осічки підряд

Ці чотири випадки утворять повну групу подій (сума їхніх ймовірностей дорівнює одиниці)

Аналізуючи отримані результати, бачимо, що ймовірність хоча б одного пострілу дорівнює сумі

Тепер розглянемо інший випадок. Припустимо, що після першого натискання на курок барабан розкрутили й знову нажали на курок.

Імовірності першого пострілу й першої осічки не змінилися - , Умовні ймовірності другого пострілу й осічки обчислюються з умови, що напроти стовбура може виявитися те ж гніздо, що й у перший раз.

Умовна ймовірність пострілу при другій спробі - якщо в перший раз був постріл, - якщо в перший раз відбулася осічка.

Умовна ймовірність осічки в другий раз - , якщо в перший раз відбувся постріл, - якщо була осічка.

Тоді:

- два постріли підряд

- перша осічка, другий постріл

- перший постріл, друга осічка

- дві осічки підряд

У цьому випадку ймовірність того, що відбудеться хоча б один постріл, дорівнює

Поиск по сайту: