Перестановки. Размещение без повторений

По определению конечное множество Х называется упорядоченным, если его элементы некоторым образом пронумерованы: Х = { X1; X2; X3; …; Xn }. Понятие упорядоченного множества – частный случай понятия кортежа. Оно выделяется из общего понятия кортежа условием, что в упорядоченном множестве все элементы различны.

Например, кортеж (1; 2; 1; 3; 1; 4) не является упорядоченным множеством, а (1;2;3;4;5) упорядоченное множество натуральных чисел.

Одно и тоже множество можно упорядочить различными способами. Множество студентов группы, например, можно упорядочить по возрасту, росту, весу, алфавиту и т.д.

Решим задачу. Сколькими способами можно упорядочить

m – множество Х? Каждое упорядочение заключается в том, что какой - то элемент получает №1, какой - то №2 и т.д., какой - то номер m. Номер 1 может получить любой из элементов множества Х, значит его можно выбрать m способами. Если первый элемент выбран, то второй элемент можно выбрать

(m –1) способами, третий (m –2) и т.д. способами. Последний элемент можно выбрать единственным способом. По правилу произведения получаем, что число упорядочений m - множества Х равно произведению.

m (m-1)(m-2) … (m-k+1) (m-k) … 2 1 (7)

Произведение первых m натуральных чисел в комбинаторике называется «m – факториал» и обозначается m!. Таким образом, число различных упорядочений m - множества Х равно m!. Различные упорядочения m – множества состоят из одних и тех же элементов и отличаются друг от друга лишь порядком следования этих элементов. При этом элементы в них не повторяются. Поэтому их называют перестановками без повторений из m – элементов. Число таких перестановок обозначают Pm (фр. слово permutation – перестановка). Таким образом,

Pm = m! (8)

С помощью формулы (8) решаются следующие задачи:

а) сколькими способами можно посадить трёх человек на одну скамейку?

Решение:

m = 3, P_m = 3! = 1 2 3 = 6;

б) сколькими способами можно расставить на книжной полке двадцать томов Вальтера Скотта?

Решение:

m = 20, P_m = 20!=1 2 3 4 5 … 18 19 20= 2 432 902 008 176 640 000 способов.

Решим более общую задачу: Сколько упорядоченных k - подмножеств можно составить из m - элементов множества Х?

Отличительной задачей от предыдущей заключается в том, что составление упорядоченного k - подмножества заканчивается, когда мы выберем k элементов при k ≤ m.

Эти упорядоченные k - подмножества называют размещениями без повторений из m- элементов по k, а их число обозначают 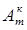Таким образом,

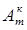= m (m -1) (m -2) … (m- k +1) (9)

Если мы умножим и разделим правую часть формулы (9) на

(m- k) (m- k -1) … 2 1, получим

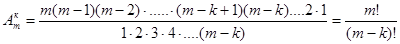
Итак, 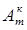= (10)

Из формулы (10) очевидно, что при m = k, имеем:

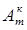= Р_m или 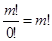Это значит, что 0! =1.

Этот вывод является одним из важных выводов комбинаторики.