 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Отношение эквивалентности. Разбиение множества на попарно непересекающиеся подмножества
Отношение между элементами множества могут обладать одним, двумя или тремя перечисленными в п. 4.3.1. свойствами или не обладать ни одним из них. Например, отношение «прямая x перпендикулярна прямой y» симметрично и антирефлексивно; отношение «x>y» транзитивно, антирефлексивно и асим- метрично; отношение x:y транзитивно, рефлексивно и антисимметрично.
Определение. Отношение R на множестве X называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
В математике выделение отношения эквивалентности связано с разбие -нием множества на попарно непересекающиеся подмножества, или классы. Отметим, что вопросы классификации важны не только для математики, но и имеют общенаучное значение.
Говорить о разбиении данного множества X на попарно непересекающ- иеся подмножества или классы можно тогда, когда одновременно выполняются следующие условия:
1) все подмножества, образующие разбиение, непусты;
2) любые два подмножества непересекаются;
3) объединение всех подмножеств есть данное множество X.
Рассмотрим на множестве дробей
отношение равенства. Его граф приведён на рис. 4.20
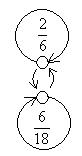
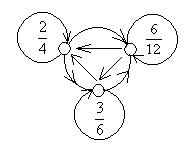
Рис.4.20
Данное отношение на множестве этих дробей рефлексивно, симметрично и транзитивно, а следовательно, является отношением эквивалентности. На рис. 4.20 хорошо видны три подмножества, на которые разбилось множество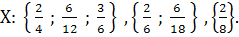 
Эти подмножества не пересекаются, а их объединение совпадает с множеством X. Таким образом, отношение «дробь x равна дроби y» разбивает множество X на классы эквивалентных дробей.
Теорема. Для того, что бы отношение R позволило разбить множество X на классы, необходимо и достаточно, что бы R было отношением эквивалентности.
Из этой теоремы следует, что если множества (классы) R(a) и R(b) (bЄR(a)) имеют хотя бы один общий элемент C, то они совпадают. Таким образом, любые два подмножества R(a) и R(b) либо совпадают, либо не пересекаются. А так как каждый элемент a принадлежит классу R(a), то получим разбиение множества X на попарно непересекающиеся подмножества.
Если отношение эквивалентности имеет название, то соответствующие название даётся и классам: множество треугольников отношения подобия разбивается на классы подобных треугольников; множество студентов отношением «быть сокурсником» разбиваются по курсам, отношение «быть одногруппником» - по группам; множество всех числовых выражений отношением «выражение х и у имеют одинаковые числовые значения» разбивается на классы, в каждом из которых находятся выражения, значения которых совпадают. Так, выражения 1+7; 5+3; 
; 2 
4; 
находятся в одном классе, а выражения 21+4; 52;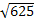 
- в другом.
Поиск по сайту: