 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Числовые множества
Множество натуральных чисел
N ={ n }={1, 2,..., n,... }.
Множество целых чисел
Z= {0, 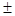 1,
1, 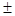 2,...,
2,..., 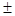 n,...}
n,...}

 Множество рациональных чисел
Множество рациональных чисел
Q=  , где
, где 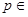 Z,
Z, 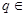 Z,
Z, 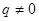
Множество действительных чисел R ={ x }
Имеет место такое последовательное включение:
 N
N 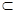 Z
Z 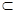 Q
Q 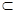 R
R
Все указанные числовые множества обладают свойством упорядочен- ности, т.е. для любых двух различных элементов а и в либо а > в, либо а < в. Кроме того, выполняется свойство транзитивности: из а > в и в > с
следует, что а > с.
Множества Q и R являются всюду плотными множествами, т.е. между любыми двумя различными элементами а и в найдется хотя бы один элемент(например, элемент с =  ).
).
Множество R обладает важным свойством непрерывности.
Пусть А ={ x } - некоторое непустое множество действительных чисел.
Множество А называют ограниченным сверху (снизу), если существует действительное число К такое, что x  К (x
К (x  К).
К).
Всякое К с указанным свойством называют верхней (нижней) гранью множества А.
Множество называют ограниченным, если оно ограничено и сверху и снизу.
Наименьшую из верхних граней множества А называют точной верхней гранью этого множества и обозначают символом sup A (супремум А).
Наибольшую из нижних граней называют точной нижней гранью этого множества и обозначают символом inf A (инфимум A).
Свойства точной верхней и точной нижней граней:
1. Для любого элемента х  А выполняется неравенство х
А выполняется неравенство х  sup A (х
sup A (х  inf A)
inf A)
2. 
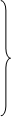 Для любого числа
Для любого числа 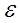 > 0 найдётся элемент х
> 0 найдётся элемент х  А такой, что х > sup A-
А такой, что х > sup A- 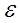 (х < inf A+
(х < inf A+  ).
).
Пример: А =[ a,в [ ={ x a  x < в }
x < в }
 В =] a,в ] = { x a < x
В =] a,в ] = { x a < x  в } - полуоткрытые интервалы.
в } - полуоткрытые интервалы.
 |
C =]  ; а ] = { x
; а ] = { x  < x
< x  a }
a }
Здесь inf A=а, sup В=в, sup С=а принадлежат указанным множествам; sup А=в, inf В=а - не принадлежат им.
Поиск по сайту: