Правило суммы

Правило суммы позволяет вычислить число элементов в объединении двух конечных множеств.

Пусть n (Х) – число элементов конечного множества Х, состоящее из n элементов (n – множество Х), а множество Y содержит m элементов (m – множество Y), т.е. n (Y) = m.

Найдём количество элементов в объединении множеств Х Y. Рассмотрим случай, когда множества не пересекаются.

Даны множества Х = { a; в; c; d }, Y = { e; f; g }.

Тогда Х Y = { a; в; c; d; e; f, g }, а их количество n (Х Y) = 4+3=7.

Нетрудно видеть, что для любых непересекающихся множеств справедливо равенство

n (Х Y)= n (X) + n (Y). (1)

Равенство (1) в комбинаторике формируют следующим образом: если элемент x можно выбрать k способами, а элемент y – m способами, причём ни один из способов выбора элемента х не совпадает со способом выбора элемента y, то выбор «x или y» можно осуществить k+m способами

Пример 1

В вазе лежат 8 яблок и 6 груш. Сколькими способами можно выбрать один плод?

Решение:

В задаче речь идёт о выборе «яблоко или груша», который можно осуществить 8+6=14 способами.

Пусть Х = { a; в; c; d; e }, а Y ={ d; e; f; g }. Множества X и Y пересекаются. Объединение множеств содержит следующие элементы:

Х Y = { a; в; c; d; e; f; g } и содержит не 9, а только 7 элементов, так как Х Y = { d;e }.

В общем случае, для любых двух конечных множеств X и Y справедливо равенство n (Х Y) = n (X) + n (Y) – n (Х Y) (2)

Пример 2 Из 30 студентов группы 25 человек успешно сдали экзамен по математике, а 23 человека – по физике. Двое студентов получили неудовлетворительные оценки по обоим предметам. Сколько студентов имеют академическую задолженность?

Решение. Пусть Х – множество студентов, не сдавших экзамен по математике, тогда их количество n (X) = 5 (30-25=5). Y – множество студентов, не сдавших экзамен по физике, их количество n (Y) = 7 (30-23=7).Согласно условию задачи число студентов в пересечение множеств X и Y равно 2, т.е.

n (Х Y) = 2. По формуле (2) найдём число студентов, имеющих академическую задолженность.

n (Х Y) = 5+7-2=10.

Для трёх конечных множеств X,Y,Z справедливо равенство

n (X Y Z)= n (X)+ n (Y)+ n (Z)- n (Х Y)- n (Х Z)- n (Y Z)+ n(X Y Z) (3)

Пример 3 В классе 40 человек. Из них 26 играют в баскетбол, 25 – занимаются плаванием, 27 – ходят на лыжах, при этом одновременно плаванием и баскетболом занимаются 15 человек, баскетболом и лыжами – 16, плаванием и лыжами – 18, Один человек от физкультуры освобождён. Сколько человек занимается всеми указанными видами спорта? Сколько человек занимается только одним видом спорта?

Решение:

В задаче рассматриваются три множества:

Множество А – учащихся, играющих в баскетбол,

Множество В – занимающихся плаванием,

Множество С – занимающихся лыжным спортом.

По условию все эти множества попарно пересекаются (Рис 2.1)

Рис 2.1

Обозначим число элементов пересечения данных множеств буквой х и определим число учащихся в каждой из непересекающихся областей.

Так как по условию задачи в классе 40 человек, то можно составить уравнение:

26+25-(33- х)+(18- х)+27-(34- х)+1=40

Отсюда получаем, что х =10. Таким образом, всеми видами спорта занимается 10 человек, только баскетболом – 5 человек (26-(31- х)), только плаванием – 2 человека (25 - (33 - х)), только лыжами – 3 человека (27-(34- х)).

Пример 4

Из 50 студентов 20 знают немецкий язык, а 15 английский. Каким может быть число студентов, знающих оба языка? знающих хотя бы один язык?

Решение.

В задаче рассматриваются множество

А – всех студентов и его подмножества:

В - знающих немецкий язык,

С – знающих английский язык.

Известно, что n (A) = 50, n (B) = 20, n (C) = 15.

Возможные отношения между множествами А, В и С можно изобразить при помощи кругов Эйлера (Рис 2.2)

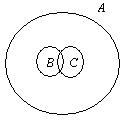
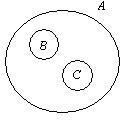
n (B C) = 0 n (B C) = 15

n (B C) = 35 Рис 2.2 n (B C) = 20

Вопрос о числе студентов, знающих оба языка, сводится к определению числа элементов в пересечении множеств В и С, а вопрос о числе студентов, знающих хотя бы один язык, - к определению числа элементов в объединении множеств В и С.

Если х- число студентов, знающих оба языка, то, используя рис 2.2, заключаем, что 0≤ х ≤15 (х є Z _o).

Если y число студентов, знающих хотя бы один язык, то 20≤ y ≤35 (y є Z_o).

Поиск по сайту: