 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Упражнения и задачи
1. Дано множество  и множество натуральных чисел N. СоответствиеRмежду элементами этих множеств – «квадрат x равен числу n», где x
и множество натуральных чисел N. СоответствиеRмежду элементами этих множеств – «квадрат x равен числу n», где x  X, n
X, n  N. Запишите множество пар, находящихся в заданном соответствии.
N. Запишите множество пар, находящихся в заданном соответствии.
Верно ли, что: 1) (-3;9) 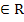
2) (0;0) 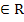
3) (-4;16) 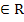 ?
?
2. Соответствие «меньше» задано между элементами множеств A  и B
и B  . Постройте график этого соответствия. Каким будет график соответствия «меньше на 1 » между элементами тех же множеств?
. Постройте график этого соответствия. Каким будет график соответствия «меньше на 1 » между элементами тех же множеств?
3. Построить график соответствия «число  меньше числа
меньше числа  на 3» между множествами.
на 3» между множествами. 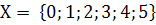 и Y
и Y  Z, если
Z, если 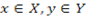 (Z - множество целых чисел).
(Z - множество целых чисел).
4. Графиком соответствия P, заданного между множествами X и Y, является прямоугольник ABCD.(Рис.4.22).
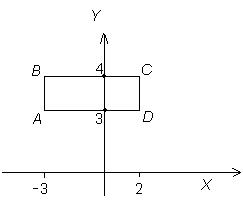 Назовите координаты трёх точек этого
Назовите координаты трёх точек этого
графика. Укажите характеристическое
свойство чисел, принадлежащих
множествам X и Y.
Рис. 4.22
5. Приведите примеры заданий из начального курса математики, при выпол- нении которых рассматриваются соответствия между:
1) множеством отрезков и множеством N;
2) множеством прямоугольников и множеством N;
3) множеством уравнений и множеством N;
6. Множество R= {(1;1),(3;0),(3;1),(4;0),(4;1),(6;1)} представляет собой соответствие между элементами множеств X ={1;3;4;6} и Y={0;1}.
Задайте соответствие  и постройте R и
и постройте R и  в одной системе координат их графики.
в одной системе координат их графики.
7. Пусть X– множество уравнений, в которых x- действительное число:
X= {x+2=5; 5x-7=3; 2(x-3)=2x-3; (x+2)(x-2)=0, (x+2)(x-2)=0 }, Y=R. Между элементами множествXиYзадано отношение P: «уравнение a имеет действительный корень y», где a  X,y
X,y  Y. Является ли отношения P отображением множества X в множестве действительных чисел R?
Y. Является ли отношения P отображением множества X в множестве действительных чисел R?
8. На рисунке 4.23 изображено некоторое множество C отрезков:
 |


|
| |||||||||||
 | |||||||||||
 |  | ||||||||||
 | |||||||||||
 | |||||||||||

Рис.4.23 Рис.4.24
Множество D =  . Между элементами множеств C и D задано отношение T: «отрезок
. Между элементами множеств C и D задано отношение T: «отрезок  имеет длину
имеет длину  »,
»,  .
.
Постройте граф отношения T и выясните, является ли отношение T отображением множества C на множестве D.
9. X – множество кругов, изображенных на рис.4.24,  . Элементы этих множеств связаны отношением T: «круг
. Элементы этих множеств связаны отношением T: «круг  имеет площадь, равную
имеет площадь, равную  »,
»,  . Постройте граф отношения T и выясните, является ли отношение T отображением множества X на множествo Y.
. Постройте граф отношения T и выясните, является ли отношение T отображением множества X на множествo Y.
10. Между множествами X ={3  4;10+2;7-2;7-7;0;6;5;(1-1)} и Y
4;10+2;7-2;7-7;0;6;5;(1-1)} и Y  Z задано отношение R: «значение выражения
Z задано отношение R: «значение выражения  равно числу
равно числу  »,
»,  .
.
Постройте граф отношения R и покажите, что оно не является отображением X в множестве Z. Выделите из множества X подмножествo A так, что бы отношение R было отображением множества A в множество Z.
11. Отношение Q: «число x больше на 2 числа y» задано на множестве B={1;3;5;7;9}.
Постройте граф и график отношения Q. Задайте отношениеQс помо- щью уравнения. Постройте графики обратного Q-1 и противоположного  отношений.
отношений.
12. Отношение S между элементами множества Y = {1;9;3;27} задано при помощи уравнения x=3y Постройте граф отношения S. Установите, какие из следующих предположений задают отношение S-1:
1) «число  меньше в 3 раза числа
меньше в 3 раза числа  »;
»;
2) «число  не больше в 3 раза числа
не больше в 3 раза числа  »;
»;
3) «число  больше в 3 раза числа
больше в 3 раза числа  ».
».
Постройте графики отношений S-1 и S1.
13. Сформулируйте свойства отношения «короче», заданного на множестве отрезков. Является ли оно отношением порядка?
14. На множестве X = {3;6;9;12;15} задано отношение «x делитель y». Покажите, что это отношение упорядочивает множество X. Чем этот порядок отличается от того, который устанавливается в множестве X при помощи отношения «больше»?
15. Верно ли, что отношение «число x непосредственно следует за числом y», заданное на N, не является отношением порядка?
16. Можно ли упорядочить множество прямых плоскости при помощи отношений: «прямая x пересекает прямую y», «прямая x перпендикулярна прямой y»?
17. На множестве X = {1;2;3;4;5;6;7;8;9;10} задано отношение R: «число x имеет один и тот же остаток при делении на 4, что и число y». Объясните, почему Rявляется отношением эквивалентности, и запишите классы разбиения множества X, определяемые этим отношением. Задайте на множестве X какое -либо отношение порядка.
Решение. Отношение Rявляется отношением эквивалентности, поскольку оно рефлексивно (можно сказать, что число имеет один и тот же остаток при делении на 4 с самим собой), симметрично (если число x имеет один и тот же остаток при делении на 4 с числом y, то и y имеет один и тот же остаток при делении на 4, что и число x), транзитивно (если число x при делении на 4 имеет тот же остаток, что и число y, а число y имеет при делении на 4 тот же остаток, что и z, то числаxиz имеют равные остатки при делении на 4).
В данном случае отношение Rразбивает множество X на классы чисел, которые при делении на 4 дают в остатке 1,2,3 и 0:
{1;5;9}, {2;6;10}, {3;7}, {4;8}.
Очевидно, на множестве X можно задать отношения порядка x>y.
 17.1. Отношение P: «число х имеет один и тот же остаток при делении на 3, что и число y» задано на множестве X = {x x
17.1. Отношение P: «число х имеет один и тот же остаток при делении на 3, что и число y» задано на множестве X = {x x  N, x
N, x  10}.Объясните, почему отношение P является отношением эквивалентности, запишите классы разбиения множества
10}.Объясните, почему отношение P является отношением эквивалентности, запишите классы разбиения множества  отношением P. Задайте на множестве X какое- либо отношение, которое не является ни отношением эквивалентности, ни отношением порядка.
отношением P. Задайте на множестве X какое- либо отношение, которое не является ни отношением эквивалентности, ни отношением порядка.
18. В множестве X={3;4;5;8} задано отношение R, график которого имеет вид:
G = {(3;3),(3;4),(4;3),(4;4),(5;5),(5;8),(8;5),(8;8)}.
Докажите, что R - отношение эквивалентности. Постройте график отношения R на координатной плоскости. Укажите его особенности.
19. На множестве X = {2;4;6;8;10} заданы отношения S: «х не больше y» и Q: «х делитель y». Докажите, что R и Q - отношения нестрогого порядка.
Постройте графы этих отношений. В чём их отличие?
Варианты индивидуальных семестровых домашних заданий (И.С.Д.З.).
Каждый студент, для того, чтобы быть допущенным к экзамену или зачёту, должен выполнить ИСДЗ. Номер варианта соответствует порядковому номеру студента в журнале. Если номер в журнале «n» превышает 20, то номер вашего варианта N=n -20.
Номера заданий и упражнений приведены в таблице № 5.1.
Семестровое задание выполняется в отдельной тетради с указанием фами- лии, номера группы, порядкового номера по журналу и номера варианта. Офор- мление работы необходимо начать с записи текста задачи и затем показать её решение с подробными объяснениями.
Допускается также работы, выполненные на листах формата А4 с обяза- тельным титульным листом, скреплёнными в один документ.
При условии правильного и подробного решения задачи за каждые две из них начисляются 1 балл из пяти возможных.
Таблица 5.1.
| Номер варианта | Упражнения и задачи с указанием страниц | |||||
| п. 1.5 страни- ца 12 | п. 2.2.1 страни- ца 21 | п. 2.3.1 страни- ца 22 | п. 2.4.1 страни- ца 25 | п. 2.5.1 страни- ца 26 | п. 4.4 страни- ца 48 | |
| 1.1; 3.2 | 1.1 | 19; 9 | ||||
| 1.2; 3.3 | 18; 8 | |||||
| 1.3; 3.4 | 17.1; 7 | |||||
| 1.4; 3.5 | 8а | 16; 6 | ||||
| 2.1; 4.1 | 8б | 15; 5 | ||||
| 2.2; 4.2 | 14; 4 | |||||
| 2.3; 5.1 | 13; 2 | |||||
| 2.4; 5.2 | 1.1 | 12; 1 | ||||
| 2.5; 5.3 | 8в | 11; 6 | ||||
| 3.1; 5.4 | 10; 7 | |||||
| 2.2; 5.2 | 8г | 8; 17.1 | ||||
| 2.4; 5.4 | 1.1 | 8д | 7; 16 | |||
| 3.1; 5.1 | 9.1 | 6; 15 | ||||
| 1.4; 3.4 | 10а | 5; 14 | ||||
| 2.1; 3.3 | 10б | 4; 13 | ||||
| 1.3; 3.5 | 10в | 2; 12 | ||||
| 1.1; 4.1 | 1.1 | 1.1 | 1; 11 | |||
| 2.3; 5.3 | 10; 19 | |||||
| 2.5; 3.2 | 10в | 9; 18 | ||||
| 1.2; 4.2 | 10г | 6; 13 |
Список литературы:
1. Виленкин Н.Я., Лаврова Н.Н., Рождественская В.Б. Задачник-практикум по математике. М.: Просвещение, 1977.
2. Викторов В.В., Худяков В.Н. Контрольные работы по математике для студентов ОЗО факультета УНК. Челябинск, ЧГПУ, 1997.
3. Виленкин Н.Я., Пышкало А.М., Рождественская В.Б. Математика. – М.: Просвещение.1977.
4. Барбаумов В.Е., Ермаков В.И. и др. Справочник по математике для экономистов; Учебное пособие / Под редакцией профессора В.И. Ермакова,
- 3 изд., переработано и дополнено. -М.:ИНФРА-М, 2007.-464 с.-(100 лет РЭА им. Г.В. Плеханова)
5. Викторов В.В. Учебно-методический комплекс, часть 1 (курс лекций) – Челябинск, 1999-68с.
Поиск по сайту: