 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Упражнения и задачи. 1.Сформулируйте условия, при которых
1. Сформулируйте условия, при которых
а) А  В
В  Ø
Ø
б) А  В = A, если:
В = A, если:
А – множество солнечных летних дней на Урале, В – множество дождливых летних дней.
Решение: а) По определению пересечения множеств А и В не пусто, если они имеют хотя бы один общий элемент, т.е. хотя бы один летний день на Урале будет и солнечным и дождливым.
б) А  В = A, только в том случае, когда В
В = A, только в том случае, когда В  А, т.е все дождливые дни обязательно должны быть попеременно с солнечным периодом в течение суток.
А, т.е все дождливые дни обязательно должны быть попеременно с солнечным периодом в течение суток.
1.1 Известно, что K – множество девушек в группе, L – множество студентов этой группы, получающих повышенную стипендию. Сформулируйте условия.
а) K  L
L  Ø б) K
Ø б) K  L = K
L = K
1.2 Множеств К определяет всех спортсменов класса, L - множество отличников.
Сформулируйте условие, при которых:
a) L  К. б) L
К. б) L  K
K  Ø
Ø
1.3 Изобразите с помощью диаграмм Эйлера – Венна следующие множества: J – универсальное множество книг в библиотеке колледжа, подмножество M – книги по математике, А – книги по алгебре, F – книги по физике, Р – книги на английском языке.
1.4 Проиллюстрируйте с помощью диаграмм Эйлера – Венна следующее высказывание:
а) некоторые чётные натуральные числа, кратные 5;
б) все числа, делящиеся на 9, делятся на 3;
в) каждое число с нулём на конце делится на 5;
г) ни одно число, запись которого оканчивается цифрой «3», не делится на 6.
2. Выясните истинность высказывания:
5 є M  (
(
 K) и 8 є M
K) и 8 є M  (
(
 K), где: М – множество нечётных натуральных чисел; Р – множество натуральных чисел, кратных 7; К – множество натуральных чисел, кратных 3.
K), где: М – множество нечётных натуральных чисел; Р – множество натуральных чисел, кратных 7; К – множество натуральных чисел, кратных 3.
Нарисуйте диаграммы Эйлера – Венна для множеств М, Р, К и укажите множество M  (P
(P  N
N  K).
K).
Решение. Число 5 – нечётное, значит 5 є М, тогда по определению объединения множеств 5 є М  (P
(P  N
N  K)-истинное высказывание.
K)-истинное высказывание.
Число 8 – чётное, не кратное 7 и 3, следовательно 8 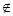 М, 8
М, 8 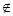 Р, 8
Р, 8 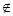 К. Так как 8
К. Так как 8 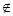 К, то и 8
К, то и 8 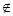 P
P  N
N  K, а значит 8 є М
K, а значит 8 є М  (P
(P  N
N  K) – ложно.
K) – ложно.
Для того, чтобы изобразить множество М, Р, К, N, нужно выяснить их взаимоотношения друг с другом.
Естественно, N – универсальное множество, а К, Р, М – его подмножества.
М и Р пересекаются, т.к среди нечётных чисел имеются числа, кратные семи: 21, 35,.... Р и К – пересекаются, т.к. среди натуральных чисел, кратных семи, имеются и кратные трём (42,...).
Пересечение K  М непусто, т.к. существует множество нечётных чисел, кратных трём.
М непусто, т.к. существует множество нечётных чисел, кратных трём.
Таким образом, имеем M 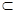 N, Р
N, Р 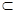 N, К
N, К 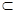 N и M
N и M 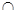 Р
Р  Ø, M
Ø, M  K
K  Ø, Р
Ø, Р 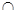 К
К  Ø
Ø
На диаграммах Эйлера-Венна этовыглядит так
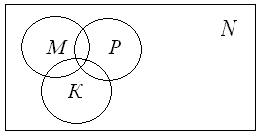
Рис. 1.10.
Изобразим теперь множество P  N
N  K т.е. элементы, которые не входят в множество Р и входят в множество К (Рис. 1.11.)
K т.е. элементы, которые не входят в множество Р и входят в множество К (Рис. 1.11.)

Рис. 1.11.
Во множество M  (P
(P  N
N  K) войдут ещё и элементы, которые принадлежат множеству М (Рис. 1.12.)
K) войдут ещё и элементы, которые принадлежат множеству М (Рис. 1.12.)

Рис. 1.12.
2.1 А- множество из N, кратных 3, В- множество чётных натуральных чисел, С – множество из N, кратных 5.
а) Выяснить истинность высказываний:
30 є А  (В
(В  С)’N, 25 є А
С)’N, 25 є А  (В
(В  С)’N. Ответ поясните.
С)’N. Ответ поясните.
б) Изобразите с помощью диаграмм Эйлера – Венна множество А  (В
(В  С)’N.
С)’N.
2.2 Даны множества: В – трёхзначные числа, В  N; С – числа, кратные 3,
N; С – числа, кратные 3,
С  N; D – множество натуральных чисел, кратных 4. Определите истинность высказываний 324 є (N
N; D – множество натуральных чисел, кратных 4. Определите истинность высказываний 324 є (N  B) \ (C
B) \ (C  D).Изобразите множество А
D).Изобразите множество А  (В
(В  С)’N.
С)’N.
2.3 Пусть К - множество треугольников на плоскости,
D - множество равнобедренных треугольников плоскости,
F - множество равносторонних треугольников плоскости,
М - множество прямоугольных треугольников плоскости.
а) Выясните, принадлежат ли множеству X = (F  M) \ (D
M) \ (D  K) равносторонние треугольники, прямоугольные прямоугольники.
K) равносторонние треугольники, прямоугольные прямоугольники.
б) Изобразите диаграммами Эйлера – Венна множества F,M,D,K и X.
2.4 Пусть: множество А – тупоугольные треугольники
множество В – прямоугольные треугольники
множество С – треугольники с углами в 60о.
Изобразите множество А  (В
(В  С). Сформулируйте его характеристическое свойство.
С). Сформулируйте его характеристическое свойство.
2.5 Дано:
В – множество натуральных делителей числа 18,
С – множество натуральных делителей числа 24.
Укажите характеристическое свойство пересечения В  С, перечислите их.
С, перечислите их.
3. Докажите, что для любых множеств А и В верно равенство: А  В’= (В\А) ’
В’= (В\А) ’
Доказательство
Докажем, что А  В’
В’  (В\А) ’. Пусть х – произвольный элемент множества А
(В\А) ’. Пусть х – произвольный элемент множества А  В’, т.е. х є А
В’, т.е. х є А  В’. По определению суммы х є А или х є В’. Если х є А, то х
В’. По определению суммы х є А или х є В’. Если х є А, то х  (В\А)’ по определению разности множеств, а следовательно, х є (В\А)’ по определению дополнения.
(В\А)’ по определению разности множеств, а следовательно, х є (В\А)’ по определению дополнения.
Если х  В’, то х
В’, то х 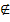 В, значит и х
В, значит и х 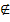 (В\А). Отсюда х
(В\А). Отсюда х 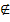 (В\А) ’ по определению дополнения.
(В\А) ’ по определению дополнения.
Таким образом, для любого элемента х из множества А  В’ справедливо: если х є А
В’ справедливо: если х є А  В’, то х є (В\А)’, т.е. А
В’, то х є (В\А)’, т.е. А  В’
В’  (В\А) ’.
(В\А) ’.
Докажем теперь, что (В\А)’ является подмножеством А  В’. Выберем элемент y из (В\А) ’, тогда y
В’. Выберем элемент y из (В\А) ’, тогда y 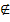 (В\А), y
(В\А), y 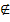 B или y
B или y 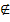 А.
А.
Если у 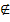 В, то у є В’, а следовательно у є А
В, то у є В’, а следовательно у є А  В’ по определению суммы.
В’ по определению суммы.
Если у є А, то у є А  В’.
В’.
Итак, из того что y є (В\А)’, следует, что у є А  В’, т.е.(В\А) ’
В’, т.е.(В\А) ’  А
А  В’.
В’.
Мы показали, что А  В’
В’  (В\А)’ и (В\А)’
(В\А)’ и (В\А)’  А
А  В’. Из определения равных множеств (х1
В’. Из определения равных множеств (х1  х2,х2
х2,х2  х1, значит х1 = х2) имеем:
х1, значит х1 = х2) имеем:
А  В’ = (В\А)’.
В’ = (В\А)’.
3.1 Докажите, что для любых множеств А и В верно равенство (А \ В)’=А’  (А
(А  В).
В).
Дайте графическую иллюстрацию с помощью диаграмм Эйлера – Венна.
3.2 Докажите, что для любых А,В и С справедливо равенство
А\(В  С)= (А\В)
С)= (А\В)  (А\С). Изобразите на диаграммах Эйлера – Венна.
(А\С). Изобразите на диаграммах Эйлера – Венна.
3.3 Докажите равенство (А  В)
В)  С = (А
С = (А  С)
С)  (В
(В  С).
С).
3.4 Докажите (А’  В’)= А
В’)= А  В’.
В’.
3.5 Докажите, что если А  В, то В’
В, то В’  А’. Дайте графическую иллюстрацию.
А’. Дайте графическую иллюстрацию.
4. Найдите пересечение, объединение и разность множеств А и В, если
 |  |
А = { x x є R, x є (-10; 7 ] }, B = { x x є R, x є [ 1; 10) }.
Изобразите множества на числовой прямой.
Решение:
Изображаем множества А и В на числовой прямой ОХ в соответствующем масштабе (Рис.1.13)

Рис.1.13
 А
А  В = {x x є R, x є [1; 7 ] }
В = {x x є R, x є [1; 7 ] }

 А
А  В = {x x є R, x є (-10; 10)}
В = {x x є R, x є (-10; 10)}
А\В = {x x є R, x є (-10; 1)}
 В\А = {x x є R, x є (7; 10 ] }
В\А = {x x є R, x є (7; 10 ] }
4.1 Используя числовую прямую, найдите пересечение, объединение и разности множеств

 а) А = { x x є Z, x > - 2 }, B = { x x є N, x ≤ 8 }
а) А = { x x є Z, x > - 2 }, B = { x x є N, x ≤ 8 }

 б) А = { x x є R, x ≥ - 2 }, B = { x x є R, x ≤ 8 }
б) А = { x x є R, x ≥ - 2 }, B = { x x є R, x ≤ 8 }

 в) А = { x x є R, 0 < x < 3.5 }, B = { x x є R, -3 < x < 1 }
в) А = { x x є R, 0 < x < 3.5 }, B = { x x є R, -3 < x < 1 }

 г) А = { x x є R, x < -1.7}, B = { x x є R, x > -1.2 }
г) А = { x x є R, x < -1.7}, B = { x x є R, x > -1.2 }
4.2 Установите, в каком отношении находятся множества А и В, если
А = { a; в; c; d }, а множество В таково:
а) B = { k; L; m }
б) B = { в; c; e; f; k }
в) B = { d; f; c; в; a }
г) B = { в; d }
д) B = { d; c; в; a }
е) B = Ø.
5. Изобразите на координатной плоскости декартово произведения Х  Y, если
Y, если

 X = { x x є N, 2 ≤ x < 5 }, Y = { y y є R, 3 < y ≤ 10 }.
X = { x x є N, 2 ≤ x < 5 }, Y = { y y є R, 3 < y ≤ 10 }.
Решение. Элементами множества X и Y являются пары чисел (x;y), в которых компонента x є X, а компонента y є Y. В данном случаеX = {2; 3; 4},а Y = (3;10 ]. Таким образом, мы должны построить все точки, у которых абсцисса х равна 2,3 или 4, а ордината y - любому числу из промежутка (3; 10]. Множество X и Y изображается в виде трёх отрезков, показанных на Рис. 1.14

Рис. 1.14
5.1 Постройте на координатной плоскости множество точек декартова произведения множеств X и Y.

 а) X = { x x є R, 0 ≤ x ≤ 7 }, Y = { y y є Z, -3 < y < 2 }
а) X = { x x є R, 0 ≤ x ≤ 7 }, Y = { y y є Z, -3 < y < 2 }

 б) X = { x x є R,
б) X = { x x є R,  = 2 }, Y = { y y є R,
= 2 }, Y = { y y є R,  ≤ 2 }
≤ 2 }

 в) X = { x x є R, -3 < x ≤ 4 }, Y = { y y є Z, 2 ≤ y ≤ 5 }
в) X = { x x є R, -3 < x ≤ 4 }, Y = { y y є Z, 2 ≤ y ≤ 5 }
г) X = R, Y = (-2; ∞)
д) X = { 1; 2; 3; 4 }, Y = [ 6; 8 ]
е) X = (- 4; -5), Y = (  ; 4 ].
; 4 ].
5.2 На координатной плоскости постройте две прямые, проходящие через точки А(3;6) и В (-2; -3) и параллельные оси OY. Выясните, декартово произведение каких множеств изображается в виде полосы, заключённой между ними?
5.3 Даны множества А = {a;в;c}, B = {1;2}, C = {2;3;4}.
a) Запишите множества A 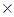 B, A
B, A  C, B
C, B  C.
C.
б) Выясните, какие элементы принадлежат множествам (A  B)
B)  (A
(A  C) и А
C) и А  (В
(В  С).
С).
в) Верно ли, что (A  B)
B)  (A
(A 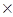 C) = А
C) = А  (В
(В  С)?
С)?
5.4 Докажите, что для любых множеств А,В,С справедливо
А  (В
(В  С)= (A
С)= (A  B)
B)  (A
(A  C).
C).
Поиск по сайту: