АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Отображения множеств. Взаимно однозначные соответствия

Читайте также:
  1. IV. Далее в этой лабораторной работе необходимо создать и сохранить запрос для отображения средних цен на все товары по таблице «Товары».
  2. Взаимное влияние личностей и ситуаций
  3. Взаимное движение капиталов
  4. Взаимное расположение в пространстве
  5. Взаимное расположение стрелочных переводов на станциях
  6. Декларирование соответствия. Схемы декларирования соответствия
  7. Диаграммы сравнения применяются для графического отображения статистических данных с целью их наглядного сопоставления друг с другом в тех или иных разрезах.
  8. Диалектический принцип взаимного перехода количественных изменений в качественные.
  9. Динамика взаимного торгового оборота США и ЕС (в млн евро)
  10. Закон взаимного перехода количественных и качественных закономерностей
  11. Закон взаимного перехода количественных и качественных изменений
  12. Коэффициент взаимной сопряженности Чупрова

Рассмотрим частный случай соответствия – отображение множеств. При соответствии R между множествами X и Y образ элемента a X может оказаться пустым, а может содержать и несколько элементов.

Отображением множества X в множество Y называется такое соответ -ствие между ними, когда образ любого элемента a X состоит из одного и только одного элемента множества Y, т.е. для любого a X найдется один и только один элемент в 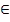Y, такой, что aRв.

 

Отображение множеств обычно обозначают следующим образом:

f: X Y, X f Y, f – символ отображения.

При отображении f элементу x соответствует элемент y пишут: f: x y или x f y, или y = f(x).

Если изобразить отображение множества X в множество Y графом, то из каждой точки множества X будет выходить одна и только одна стрелка(рис. 4.6), а график отображения f: X Y

а x

в y

X Y

с z

 

d t

 

Рис. 4.6 Рис. 4.7

 

не может содержать двух различных пар (a; У1) и (a; У2) с одной и той же первой компонентной (иными словами от любой вершины графа исходит только одно ребро).

Рассмотрим примеры отображений.

Пример 1. Пусть X – множество студентов в аудитории, Y – множество компьютеров в аудитории, причём каждый студен сидит за своим компьютером. Соответствие «Студент x сидит за компьютером y» задает отображение f: X Y. Образом студента x является компьютер, за которым он сидит.

Пример 2. Пусть X - множество точек отрезка AB, а Y – множество точек прямой MN (рис. 4.7). Поставим в соответствии каждой точке P отрезка AB точку P1 на MN, где P1 есть основание перпендикуляра (PP1 MN). Так как каждой точке на AB можно поставить только одну точку в соответствие на прямой MN, то данное соответствие является отображением множества точек отрезка AB в множестве точек на MN. Отрезок A1B1 есть образ отрезка AB на прямую MN.

Пример 3. Каждой точке окружности A поставим в соответствие точку A1 её диаметра, такую, что прямая AA1 есть перпендикуляр к диаметру MN. Получим отображение окружности на её диаметр. (рис.4.8)

а x

A в y B

с z

d t

e p

f

 

Рис.4.8 X Y

 

Рис.4.9

 

В математике с понятием отображения связывают понятие функции. Если из множества X данного соответствия выделить подмножество тех элементов, для которых имеется соответствующий образ у множества Y, получим функциональную зависимость y = f(x) (рис. 4.9). Здесь множество A = { a; b; c; d } – область определения функции, причем A < X. Множество B = { x; y; z }, т.е. тех y Y, которые являются образами всех x области определения, называется множеством значений функции и пишут y = f (x).

Из всевозможных соответствий и отображений особое внимание в математике уделяется таким, при которых каждому элементу множества x X сопоставляется единственный элемент множества Y, и каждый элемент множества Y соответствует только одному элементу из множества X. Такие множества называются взаимно однозначными. Рассмотримпримеры таких графов для взаимно однозначных соответствий.

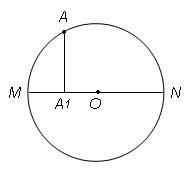
Пример 4. Пусть X = { a; b; c; d }, Y= {1; 2; 3; 4}.

Соответствие между элементами этих множеств установлено при помощи связных компонент графа на рис. 4.10. Данное соответствие между множествами взаимно однозначное.

 

 

 

 

 

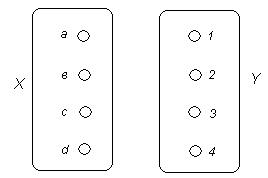
Рис. 4.10 Рис. 4.11

 

Пример 5. X – множество углов треугольника ABC, а Y – множество его сторон. Соответствие, при котором углу ставится в соответствии противо- лежащая ему сторона, будет, естественно взаимно – однозначным.

Если между множествами X и Y можно установить взаимно однозначное соответствие, то говорят, что множества X и Y являются равномощными или эквивалентными и пишут X ~ Y.

Эквивалентными могут быть как конечные, так и бесконечные множества. Для конечных равномощных множеств существует определение равночисленные множества, т.к. они содержат одинаковое количество элементов.

Рассмотрим два бесконечных множества: множество N натуральных чисел и множество Y их квадратов. Поставим в соответствие натуральному числу n его квадрат n2 (рис. 4.11.), получим взаимно-однозначное следствие Y~ N, но множество Y является подмножеством множества N, то есть равномощными оказались множество и его собственное подмножество.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.008 сек.)