Расписание экзаменационной сессии

Таблица №1

Группа дата	23.12.2009	24.12.2009	25.12.2009	27.12.2009
ХТ-81	Химия		Математика
РБ-81		Физика		Математика
ХТ-82	Математика		Радиохимия

Таким образом, соответствие между конечными множествами можно задать с помощью таблиц. Кроме таблиц соответствие между конечными множествами задаются графиками соответствия или ориентированными графами.

Граф G соответствия R есть совокупность всех пар (x; y), где x X, y Y для которых предикат R(x; y) принимает истинные значения.

Соответствие «Группа х сдает экзамен в день y» представим в виде ориентированного графа (рис. 4.1).

ХТ-81 Р1 Р4 23.12.09 а t

Р5 24.12.09 в x

РБ-81 Р2

Р6 25.12.09 с y

ХТ-82 Р3 Р7 27.12.09 d z

X Y

Рис. 4.1 Рис. 4.2

На рис 4.2 изображен граф соответствия между множествами X и Y. Возьмем какую - нибудь точку из множества X, например точку a, и все стрелки (рёбра графа), выходящие из этой вершины. Множество концов стрелок называют образом элемента a (вершины a) во множестве Y и обозначают R(a); при этом

R(a) = {t; y; z}, R(в) = Ø, R(c) = {x}, R(d) = {t; z }.

Множество начала рёбер называют прообразом элемента y в множестве X и обозначают R^-1(y).

Для элемента t, например, полный прообраз

R^-1(t) = {a; d}, для x, y, z соответственно R^-1 (x) = {c}, R^-1(y) = {a}, R^-1(z) = {a; d}.

Множество A всех элементов из X, имеющих непустые образы, называют множеством определения соответствия R.

Множество B всех элементов из Y, имеющих непустой полный прообраз, называют множеством значений соответствия R.

Для соответствия графа на рис. 4.2 множество A и B определены A = {a; c; d}, B = {x; y; z; t}.

Чтобы представить соответствие между элементами числовых множеств X и Y на координатной плоскости yOx в виде графика, нужно изобразить все пары чисел, находящихся в соответствии R, точками на плоскости.

Пример 1. Построить график соответствия «x>y», где X = {1; 2; 3; 4}, y Y = {1; 2}.

Решение. Запишем пары чисел, находящихся в заданном соответствии для предиката x > y:

(2; 1), (3; 1), (4; 1), (3; 2), (4; 2). Изобразим элементы множества X на оси Ox, элементы множества y на оси Oy. Каждую из полученных пар поместим на координатную плоскость y Ox, получим график соответствия «x >y» (рис. 4.3).

Y

2

1

X

1 2 3 4

Рис. 4.3

Пример 2. Построить график соответствия «x > y», где x X = R, y Y = R.

Решение. Все числа, у которых абсцисса равна ординате x = y, располагаются на прямой y = x, т.е. на биссектрисе 1 ^–го и 3^–го координатных углов (рис. 4.4).

Y

расположены под биссектрисой, например точка

«x > y», заданного на множестве действительных

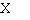чисел R, вляется полуплоскость, расположенная под биссектрисой 1^–го и 3^–го координатных углов; сама биссектриса (прямая y = x) этой полуплоскости не принадлежит.

Рис. 4.4

Рассмотрим обратное соответствие. Пусть задано соответствие xRy между множествами X и Y. Обратным ему называют соответствие ySx междумножествами Y и X, такое, что ySx в том и только в том случае, когда xRy. Обратное соответствие обычно обозначают y .

Обратным для соответствия «число x больше числа y» будет соответствие «число y меньше числа x», т.е. x > y тогда и только тогда, когда y < x. Чтобы получить график обратного соответствия R^-1, надо взять график прямого соотве-

тствия R и поменять компоненты в каждой паре. Граф соответствия R^-1 получается измением направления всех стрелок на обратное в графе соответствия R.

Выясним, как связаны между собой графики прямого и обратного соотве- тствий при изображении их в прямоугольной системе координат. Рассмотрим следующий пример.

Между множествами X = {2; 4; 6; 8; 9; 10} и Y = {2; 3; 5} задано соответствие «число x делится на число y». График этого соответствия имеет следующий вид:

R = {(2; 2), (4; 2), (6; 2), (8; 2), (10; 2), (6; 3), (9; 3), (10; 5)}.

Обратное соответствие «число y является делителем числа x» запишем

R^-1 = {(2; 2), (2; 4), (2; 6), (2; 8), (2; 10), (3; 6), (3; 9), (5; 10)}.

Легко видеть, что на координатной плоскости графики соответствий R и R^-1 симметричны относительно прямой y = x (рис.4.5)

Рис.4.5

Может случится, что графики соответствий xPy и xQy дополнительные множества в X Y. Такие соответствия называются противоположными, их обозначают xP’y, xQ’y и т.д. Например, соответствие «число x больше числа y» противоположно соответствию «число x не превосходит числа y».

Поиск по сайту: