 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Подмножества. Диаграммы Эйлера-Венна
|
Читайте также: |
Множество В называют подмножеством А тогда и только тогда, когда каждый элемент B принадлежит множеству А. Так, множество студентов группы БИ-81-2 является подмножеством множества студентов дневного отделения колледжа, которое, в свою очередь, является подмножеством множества всех студентов данного колледжа и т.д.
Высказывание «Множество В является подмножеством множества А» записывается так: 
Эквивалентное высказывание «Множество А включает в себя подмножество В»: 
Для наглядности отношение между множествами изображают с помощью диаграмм (кругов) Эйлера-Венна. Если , то рисуют
Рис. 1.1.
Утверждение, если 
и 
, то 
(свойство транзитивности) можно изобразить так:
Рис. 1.2.
Из определения подмножества очевидно, что каждое множество А является подмножеством самого себя, т.е. 
. Множество Ø есть подмножество любого множества, т.е. Ø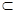 
А. Два последних подмножества А иØ для множества А называются несобственными подмножествами; все остальные, если они существуют, являются собственными подмножествами А.
Дадим другое определение равных множеств: Множества А и В равны (А=В) тогда и только тогда, когда и
Если множество А конечно и содержит m – элементов, то число его подмножеств равно 2 m. Пример: множество D ={12,13,14} содержит 8 подмножеств (23=8), из них 6 собственных множеств: {12},{13},{14},{12;13}, {12;14},{13;14} и два несобственных: {12,13,14} и Ø.
Если рассматривать некоторую систему множеств А, В,С, D, …то множество 
называют универсальным для этой системы, если каждое множество системы является подмножеством 
, т.е. 
, 
, 
, 
,...
Пример: А ={2,7,11}, В ={10,8,3,5}, С – множество чётных чисел {2,4,6, …, 2n, …}. За универсальное множество для данной системы из трёх множеств можно принять множество всех натуральных чисел = N, или ={x x 
N }.
Если множество студентов колледжа для нас будет универсальным, то оно включает в себя множество студентов 1го, 2го, 3го, 4го курсов. На диаграмме Эйлера-Венна множество обозначают прямоугольником, а его подмножества - кругами
 |
Рис.1.3
 |
Поиск по сайту: