 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Сочетания без повторений
Сколько неупорядоченных подмножеств, содержащих по k – элементов каждое, можно составить из элементов данного m - множества Х? В подмножествах элементы не повторяются, а порядок их следования не существенен. Такие подмножества называют сочетаниями без повторений из m - элементов по k. Их число обозначают 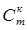 (от фр. слова combination – сочетание).
(от фр. слова combination – сочетание).
Число упорядоченных множеств 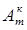 в k! раз больше, чем неупорядочен- ных, т.е.
в k! раз больше, чем неупорядочен- ных, т.е. 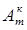 = k!
= k! 
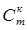 , таким образом,
, таким образом, 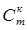 = (11)
= (11)
Подставим в формулу (11) выражение (10):
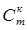 = (12)
= (12)
Пример: Сколькими способами можно выбрать делегацию в 5 человек из группы, содержащей 12 человек?
Решение: Поскольку порядок членов делегации роли не играет, то задача решается по формуле (11), где k = 5, m = 12:

Свойство чисел 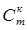
1. 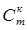 =
=  (13)
(13)
2. 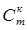 =
=  +
+  (14)
(14)
3.  =
=  = 1 (15)
= 1 (15)
4.  = 0 (16)
= 0 (16)
5. При k > m 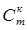 = 0 (16’)
= 0 (16’)
Поиск по сайту: