Свойствa отношений

Пусть на множестве Х задано отношение R. Определение. Отношение R называется рефлексивным, если для любых х из множества Х истинно хRх.

Другими словами, отношение R рефлексивно, если о любом элементе х Х можно сказать, что он находится в отношение R с самим собой.

Рефлексивными будут следующие отношения. Во множестве натуральных чисел N отношения «равенства» и «кратности»: «число х равно числу y», «число х кратно числу y». На множестве прямых – отношения параллельности: «прямая х параллельна прямой y». Во множестве геометрических фигур – отношение конгруэнтности, поскольку каждая фигура конгруэнтна самой себе.

Если отношение R рефлексивно, то в каждой вершине графа имеется петля (рис.4.14). Справедливо и обратное: если в каждой вершине графа имеется петля, то этот граф представляет рефлексивное отношение.

Существуют и антирефлексивные отношения,т.е. такие, тогда ни один элемент х Х не находится в отношении R с самим собой. Во множестве прямых таким свойством обладает отношение «прямая х перпендикулярна прямой у», т.к. ни одна прямая не перпендикулярна самой себе.

Определение. Отношения R называется симметричным, если для любых элементов х и у множества Х из хRу следует уRх.

Симметричными являются отношения параллельности и перпендикулярности на множестве прямых плоскости: «если прямая х параллельна(перпендикулярна) прямой у, то и прямая у параллельна(перпендикулярна) прямой х».

Отношения конгруэнтности во множестве фигур или равенства на множестве чисел также симметричны. Граф симметричного отношения обладает следующей особенностью: для каждой вершины х и у существует циклическая дуга (рис.4.16)

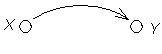
Рис.4.16 Рис.4.17

Рис.4.18

Рис.4.19

Определение. Отношение R называется асимметричным, если ни для каких элементов х и у множества Х не может случится, что одновременно хRу и уRх.

Примером асимметричного отношения являются отношения строгого порядка «х>у», «х<у», заданного на множестве действительных чисел. Граф асимметри- чных отношений представлен на рисунке 4.17

Определение. Отношение R антисимметрично, если хRу и уRх одновременно выполняется в том и только в том случае, когда х=у. Антисимметричное отношение – это объединение асимметричного отношения с отношением равен- ства (тождества).

Антисимметричные отношения являются отношениями нестрогого порядка «х≥y» и «х≤y». Граф антисимметричного отношения представлен на рис.4.18

Определение. Отношение R называется транзитивным, если для любых элементов х,у,z из множества X из того, что хRу и уRх, следует что хRz.

Во множестве отрезков транзитивным будет отношение «отрезок х длиннее (короче) отрезка у»:если отрезок х длиннее (короче) отрезка у и отрезок у длиннее (короче) отрезка z, то отрезок х длиннее (короче) отрезка z. Граф такого отношения представлен на рис. 4.19.

Поиск по сайту: