 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Подграфы. Операции над графами
Рассмотрим граф G =(P,A) с множеством вершин P и множеством рёбер А. Граф G’= (P’,A’) называется подграфом графа G, если P ’ и A ’ являются подмножествами Р и А, при чем ребро содержится в A’ только в том случае, если его концевые вершины содержатся в Р’.
Пусть Р’ – некоторое подмножество множества вершин графа G =(P,A) и пусть A’ – множество всех рёбер графа G, концевые вершины которых входят в Р’. Тогда граф G ’=(P’,A’) называется вершинно-порождённым подграфом графа G.
Обозначим через A’ некоторое подмножество множества рёбер графа G =(P,A), и пусть P ’ есть множество всех вершин графа G, инцидентных рёбрам из A ’. Тогда граф G’ =(P’,A’) называется рёберно-порожденным подграфом графа G.
На рис. 3.4 изображены вершинно-порожденный подграф G1 графа G, представленного на рис.3.1 (множество вершин Р1,Р3,Р4) и рёберно-порожденный подграф G2 того же графа G (множество рёбер £1, £3, £4, £ 6)


Рис.3.4
Операции над графами:
1. Объединением графов G1 =(P1,A1) и G2 =(P2,A2) называется граф G=G1  G2, множество вершин которого есть объединение множеств вершин графов G1 и G2 (P= P1
G2, множество вершин которого есть объединение множеств вершин графов G1 и G2 (P= P1  P2), а множество рёбер является объединением множеств рёбер этих графов (A=A1
P2), а множество рёбер является объединением множеств рёбер этих графов (A=A1  A2).
A2).
 2. Пересечением графов G1 и G2 называется граф G=G1∩G2, множество вершин которого есть пересечение P1∩P2, а множеством рёбер- пересечение A1∩A2.
2. Пересечением графов G1 и G2 называется граф G=G1∩G2, множество вершин которого есть пересечение P1∩P2, а множеством рёбер- пересечение A1∩A2.
3. Кольцевой суммой двух графов называется граф G1 + G2, порожденный на множестве ребер (А1  А2)\(А1∩А2), т.е. на множестве ребер, присутствующих либо в G1, либо в G2, но не принадлежащих их пересечению G1∩G2.
А2)\(А1∩А2), т.е. на множестве ребер, присутствующих либо в G1, либо в G2, но не принадлежащих их пересечению G1∩G2.
 Очевидно, что все эти три операции коммутативны. На рис.35 изобра -жены графы: G1,G2, G1
Очевидно, что все эти три операции коммутативны. На рис.35 изобра -жены графы: G1,G2, G1  G2; G1∩G2, G1 + G2.
G2; G1∩G2, G1 + G2.


 G1 G2
G1 G2
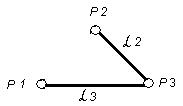
 G1∩G2
G1∩G2
 G1
G1  G2 G1 + G2
G2 G1 + G2
Рис.35
Поиск по сайту: