 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Булевы операции
Отношения между именами создают основу для логических операций с ними. Результат операций – новые имена. Операции, к описанию которых мы приступаем, называются булевыми операциями – по имени английского ученого Дж.Буля (1815-1864), одного из основоположников математической логики.
Булевы операции – это операции с объемами имен. К важнейшим из них относятся сложение, умножение и дополнение.
Сложение объемов A и В – это логическая операция, в результате которой образуется новый объем, состоящий из предметов, относящихся хотя бы к одному из объемов А и В.
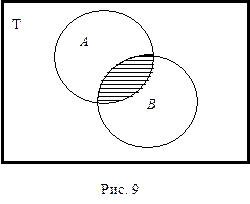
|
|
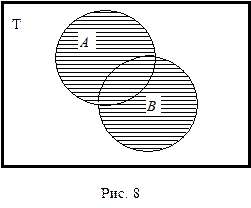
Результат операции сложения называется логической суммой и обозначается выражением АÈВ. Эту, как и прочие операции, рассмотрим на одном и том же конкретном примере объемов с иллюстрацией на круговых схемах (рис. 8-10). Результаты операций отмечены штриховкой.

|
Пусть речь идет о тыквах, и совокупность всех тыкв – универсум Т (от лат. Totum – целое). По каким-то соображениям выделены: а) тыквы весом не меньше 3 и не больше 5 кг, что соответствует объему A на круговых схемах; б) тыквы весом не меньше 4 и не больше 6 кг, что соответствует объему В на круговых схемах. Тогда логическую сумму объемов этих тыкв составят тыквы весом от 3 до 6 кг (рис. 8).
Умножение объемов A и В – логическая операция, в результате которой образуется новый объем, состоящий из предметов, относящихся как к объему A, так и к объему В. Результат называется логическим произведением и обозначается выражением AÇВ.
В нашем случае логическое произведение объемов A и В – это тыквы от 4 до 5 кг (рис. 9).
Исключение объема B из объема A – логическая операция, в результате которой образуется новый объем, состоящий из предметов объема A и не состоящий из объема B. Результат этой операции называется логической разностью и обозначается выражением A-B.
Наконец, дополнение объема A – это логическая операция, в результате которой образуется новый объем, состоящий из предметов универсума Т, не относящихся к объему A. Результат этой операции называется логическим дополнением и обозначается выражением A¢. Дополнением к тыквам весом от 3 до 5 кг будет весь универсум тыкв Т, за исключением тыкв от 3 до 5 кг (рис. 12).
Из приведенных определений видно, что существует соответствие между булевыми операциями и операциями (функторами) логики высказываний. В частности, сложению соответствует слабая дизъюнкция, умножению – конъюнкция, дополнению – отрицание.

Булевы операции подчиняются определенным законам:
| AÈA=A | идемпотентность сложения; |
| AÈВ=ВÈA | коммутативность сложения; |
| (AÈВ)ÈC=AÈ(BÈC) | ассоциативность сложения; |
| AÇA=A | идемпотентность умножения; |
| AÇВ=ВÇA | коммутативность умножения; |
| (AÇВ)ÇC=AÇ(BÇC) | ассоциативность умножения; |
| (АÈВ)ÇC=(AÇС)È(BÇC) | Дистрибутивность умножения относительно сложения; |
|
| (AÇВ)ÈC=(AÈС)Ç(ВÈC) | Дистрибутивность сложения относительно умножения. |

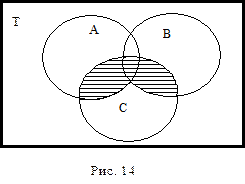
Законы ассоциативности гласят, что в выражениях вида A È В È С и A Ç В Ç С расположение скобок не играет роли, так что их можно вообще опускать (рис. 13 и 14). Однако в таких выражениях, как (A È В)Ç С или A È(В Ç С) – расположение скобок играет существенную роль. Пусть, например, A – объем имени «мужчина», B – объем имени «женщина», С – объем имени «врач». Тогда A È B – объем имени «человек», (A È B)ÇС – объем имени «врач» (рис.15, горизонтальная штриховка); В Ç С – объем имени «женщина-врач», A È(B Ç С) – объем имени, обозначающего всех людей, за исключением женщин, которые не являются врачами (рис. 15, вся штриховка).

|

|



|


| (A B)¢=A¢ Ç B¢ (рис. 24) | - 1-й закон де Моргана |
| (A Ç B)¢ = A¢ B¢ (рис. 25) | - 2-й закон де Моргана |
(A È B)¢=A¢ Ç B¢ (рис. 24);
(A Ç B)¢ = A¢ È B¢ (рис. 25).
Поиск по сайту: