 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Непосредственные силлогистические выводы
Cиллогистика – это теория дедуктивного вывода, построенного на основе высказываний вида SaP, SeP, SiP, SoP. Выводы в силлогистике подразделяются на непосредственные и опосредованные. Они отличаются друг от друга по числу посылок, из которых получается заключение.
Вывод, в котором заключение получается из одной посылки, называется непосредственным. К непосредственным: вывод по логическому квадрату, обверсия, конверсия, контрапозиция.
Руководствуясь отношениями, фиксируемые диаграммой, которая называется логическим квадратом, можно сформулировать следующие правила вывода:
а) в соответствии с отношением противоречия:

б) в соответствии с отношением противности:

в) в соответствии с отношением частичной совместимости:

г) в соответствии с отношением подчинения (следования):


В качестве иллюстраций к этим правилам можно воспользоваться примерами из предыдущего параграфа.
Обверсия (лат. – превращение) – непосредственный вывод, в процессе которого предикат посылки заменяется на противоречащее ему имя (т.е. дополняющее его) и изменяется ее качество, т.е. утвердительная посылка заменяется на отрицательную и наоборот. При этом могут быть использованы следующие правила:

Например, из истинного высказывания «Все металлы электропроводны» (SaP) путем обверсии можно получить высказывание «Ни один металл не является неэлектропроводным» (Se Р¢), из истинного высказывания «Некоторые спортсмены выносливы» (SiP) можно получить высказывание «Некоторые спортсмены не являются невыносливыми» (SоP ¢), и т.д.
Путем обверсии знание об отношении S к P обогащается знанием отношения S к имени, противоречащим P, или дополняющим P, что в ряде случаев позволяет более точно и однозначно понимать выражаемые мысли.
Конверсия (лат. – обращение) – непосредственный вывод, в заключении которого субъектом является предикат, а предикатом – субъект исходного высказывания-посылки. Это означает, что при конверсии происходит преобразование атрибутивных высказываний путем перестановки S и P местами. Качество посылки при этом остается неизменным.
Правила конверсии:

Первые из двух правил называются правилами конверсии обычной, или конверсией без ограничения, при которой происходит преобразование общей посылки в общее заключение и преобразование частной посылки в частное заключение. Например: «Ни одна планета не светит собственным светом (SeP), следовательно, ни одно тело, светящееся собственным светом, не есть планета (PeS)»; «Некоторые европейские государства являются королевствами (SiP), следовательно, некоторые королевства являются европейскими государствами (PiS)».
Вывод по третьему правилу называется конверсией с ограничением, поскольку здесь общая посылка преобразуется в частное заключение. Например: «Все студенты – учащиеся (SaP), следовательно, некоторые учащиеся – студенты (PiS)».
Как видим, конверсия применяется к высказываниям вида SaP, SeP и SiP. К высказываниям вида SoP в разговорных процессах конверсия не применяется, поскольку получающаяся конструкция имеет явно искусственный характер и может вести от истинной посылки к ложному заключению (например, «Некоторые птицы не являются певчими, следовательно, ни одна певчая птица не является некоторой (а может быть, и всякой) птицей»).
Контрапозиция (лат. – противопоставление) являются операцией, производной от обверсии и конверсии. При полной контрапозиции заключение имеет то же качество, что и посылки. Частичная контрапозиция ведет к заключению, качество которого отлично от качества посылки.
Частичная контрапозиция – вывод, при котором в заключении субъект выражается именем, противоречащим предикату посылки (дополняющим его), а на место предиката становится ее субъект; при этом посылка изменяет свое качество. Частичную контрапозицию можно осуществить путем последовательного применения превращения и обращения. Так, исходное высказывание «Все жидкости упруги» сначала превращается в высказывание «Ни одна жидкость не является неупругой». Затем путем обращения последнего получается высказывание «Ни одно неупругое тело не есть жидкость». Это и есть заключение частичной контрапозиции, дающей дополнительное знание об отношении не-P к S. Высказывание вида SiP посредством контрапозиции не преобразуется.
Правила частичной контрапозиции:
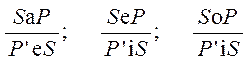
Полная контрапозиция – вывод, при котором в заключении субъект выражается именем, противоречащим предикату посылки, а предикат – именем, противоречащим субъекту посылки; при этом качество заключения не изменяется.
Полную контрапозицию можно осуществить, применив к результату, полученному при частичной контрапозиции, правило обверсии. Так, в предыдущем примере мы получили заключение «Ни одно неупругое тело не есть жидкость». Применив к нему правило обверсии:

мы, таким образом, произведем полную контрапозицию и получим заключение «Всякое неупругое тело суть не жидкость».
Правила полной контрапозиции:
 .
.
Таким образом, если превращение и обращение служат раскрытию свойств S и P, то контрапозиция – свойств их дополнений S ¢ и P¢.
В непосредственных выводах необходимо соблюдать следующее правило: термин, не распределенный в посылке, не может быть распределен в заключении. Поэтому из высказываний вида SaP при обращении выводится высказывание вида PiS, а не PaS. Ошибка, возможная как результат нарушения этого правила, называется «незаконное расширение термина». Термин же, распределенный в посылке, может оказаться нераспределенным в заключении, как это имеет место, например, в выводах по логическому квадрату при переходе от общих к частным высказываниям того же качества.
Упражнения:
1. Докажите производность правил контрапозиции (полного и частичного).
2. Произведите обверсию следующих высказываний:
a) Все судьи – юристы;
b) Некоторые государства не проводят независимую внешнюю политику;
c) Некоторые предприятия являются негосударственными;
d) Пауки не являются насекомыми.
3. Произведите конверсию следующих высказываний:
a) Ни одно насекомое не имеет более трех пар ног;
b) Некоторые существительные – слова, изменяющиеся по падежам;
c) Все неисследованное пленяет воображение.
4. Выведите заключение путем полной контрапозиции из следующих посылок:
a) Вcе философские произведения – мировоззренческие;
b) Некоторые государственные предприятия не являются рентабельными;
c) Все справедливые благородны;
d) Ни один мужественный не боязлив.
5. Кто был неправ в следующем диалоге? Какая логическая ошибка им допущена?
«– Так бы и сказала, – заметил мартовский Заяц. – Нужно всегда говорить то, что думаешь.
– Я так и делаю, – поспешила объяснить Алиса. – По крайней мере, я всегда думаю то, что говорю...а это одно и то же.
– Совсем не одно и то же, – возразил Болванщик. – Так ты, чего доброго, скажешь, будто «Я вижу то, что ем» и «Я ем то, что вижу», – одно и тоже» (Л.Кэрролл. Приключения Алисы в Стране чудес).
6. Можно ли произвести конверсию следующего высказывания: «Некоторые государства не проводят независимую внешнюю политику»?
7. Можно ли осуществить контрапозицию высказывания «Некоторые спортивные судьи - юристы»?
8. Какое правило нарушено в следующем рассуждении: «Все гениальное просто, следовательно, все простое гениально»?
9. Какое из следующих высказываний противоречит высказыванию “Всякая взятка – преступление»:
a) Ни одна взятка не есть преступление;
b) Всякая взятка – плата за услугу;
c) Некоторые взятки – преступления;
d) Всякая взятка – прибавка к зарплате.
10. Правильным ли является рассуждение: «Если истинно, что кто-то есть человек и нечеловек, то ясно, что истинно также то, что он не есть ни человек, ни не человек» (Аристотель).
Поиск по сайту: