Берков В.Ф

Определение4. Пусть функция f(х) определена прямой 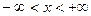и интегрируема на каждом сегменте, принадлежащем этой прямой. Будем говорить, что функция f(х) интегрируема по Коши, если существует предел .

Этот предел мы будем называть главным значением несобственного интеграла от функции f(х) (в смысле Коши) обозначать символом V. р.

V. р. =

При м ер 1. Найдем главное значение интеграла от функции x. Поскольку в силу нечетности х,

=0, то V. р. =0

Точно так же заключаем, что V. р. =0.

Справедливо следующее

Утверждение 6. Пусть функция f(х) интегрируема на каждом сегменте прямой 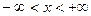. Если эта функция f (х) нечетна, то она интегрируема по Коши и главное значение интеграла от нее равняется нулю.

Если функция f(х) четна, то она интегрируема по Коши тогда и только тогда, когда сходится несобственный интеграл

(4.1)

Первая часть этого утверждения является очевидной. Для доказательства второй части достаточно воспользоваться равенством = ,справедливым для любой четной функции, и определением сходимости несобственного интеграла (4.1)

Понятие интегрируемости по Коши можно ввести и для несобственных интегралов второго рода в случае, когда особая точка является внутренней точкой сегмента, по которому производится интегрирование.

Определение5. Пусть функция f(х) определена на сегменте [ а, b ], кроме, быть может, точки с, а<с<b, и интегрируема на любом сегменте, принадлежащем либо [ а, с), либо (с,b ]. Можно говорить, что функция f(х) интегрируема по Коши, если существует предел

называемый главным значением интеграла в смысле Коши.

Пример 2. Функция не интегрируема на сегменте[ а, b ], а<с<b, в несобственном смысле, однако она интегрируема по Коши. При этом

Литература: 1, с.370-385; 7,с. 552 – 595; 10,с. 482 – 500

Контрольные вопросы и задания:

1. Сформулируйте определение несобственного интеграла первого рода.

2. Сформулируйте и докажите Критерий Коши сходимости несобственного интеграла первого рода.

3. Сформулируйте и докажите общий признак сравнения несобственного интеграла первого рода.

4. Сформулируйте и докажите частный признак сравнения.

5. Сформулируйте определение абсолютной сходимости несобственного интеграла первого рода.

6. Сформулируйте определение условной сходимости несобственного интеграла первого рода.

7. Сформулируйте и докажите признак Дирихле – Абеля.

8. Сформулируйте определение несобственного интеграла второго рода.

9. Сформулируйте и докажите Критерий Коши сходимости несобственного интеграла второго рода.

10. Сформулируйте определение главного значения несобственного интеграла.

УДК 16

ББК 87.4

Б48

Серия основана в 2001 году

Рекомендовано к изданию Комиссией по приемке и аттестации электронных версий учебных и учебно-методических материалов Академии управления при Президенте Республики Беларусь.

Печатается по решению редакционно-издательского совета Академии управления при Президенте Республики Беларусь.

Берков В.Ф.

Б48 Логика: Курс лекций / Берков В.Ф. – 2-е изд., стер. – Мн.:Академия управления при Президенте Республики Беларусь, 2005. – 264 с.

ISBN 985-457-393-1

Курс лекций предназначен для студентов системы открытого образования Академии управления при Президенте Республики Беларусь, обучающихся по специальности "Государственное управление и экономика".

УДК 16

Поиск по сайту: