АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Упражнения и задачи. 1. Сколькими способами можно выбрать 3 ленты из пяти лент различных цветов?

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Ситуационные задачи и тестовые задания.
  3. I. СТРОЕВЫЕ УПРАЖНЕНИЯ
  4. II. Основные задачи и функции
  5. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  6. II. Цель и задачи государственной политики в области развития инновационной системы
  7. III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)
  8. VI. ДАЛЬНЕЙШИЕ ЗАДАЧИ И ПУТИ ИССЛЕДОВАНИЯ
  9. АКРОБАТИЧЕСКИЕ УПРАЖНЕНИЯ
  10. АКРОБАТИЧЕСКИЕ УПРАЖНЕНИЯ
  11. Аналитические возможности, задачи и основные направления анализа СНС
  12. БАЛАНС КОММЕРЧЕСКОГО БАНКА, ЦЕЛИ И ЗАДАЧИ ЕГО АНАЛИЗА

1. Сколькими способами можно выбрать 3 ленты из пяти лент различных цветов?

Решение: Так как порядок выбора лент не играет роли, то в задаче речь идёт о выделение из множества, в котором m = 5 элементов трёхзначных подмножеств k = 3, т.е по формуле (12) имеем

1.1 Сколькими способами можно выбрать четыре краски из шести различных?

2. В шахматном турнире принимают участие 12 шахматистов. Сколько будет сыграно партий, если любые два участника встретятся между собой один раз?

3. В скольких точках пересекаются диагонали выпуклого шестиугольника, если никакие три из них не пересекаются в одной точке?

4. У одного человека есть 8 книг по искусству, а у другова-6 книг. Сколькими способами они могут обменять три книги одного человека на три книги другого человека?

5. В взводе 5 сержантов и 50 солдат. Сколькими способами можно составить парад из одного сержанта и трех солдат?

6. Рота состоит из трех офицеров, 6 сержантов и 60 рядовых. Сколькими способами можно выделить из них отряд, состоящий из одного офицера, двух сержантов и 20 рядовых?

7. На выпускном вечере присутствуют 12 девушек и 15 юношей. Сколькими способами можно выбрать из них 4 пары для танца?

 

8. Докажите равенства

а) + + =

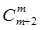б) + +…+ +…+ =

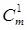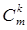в) - =

г) + + +…=2m-1

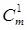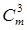д) + + +…=2m-1

9. Решить систему уравнений

 

=

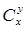=66

Решение. Решим второе уравнение: , или 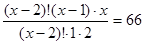,или х2-х-132=0 (х1=-11;х2=12)

Так как х>2,то окончательно, х=12. Подставим х=2 в уравнение первое: ,или . Тогда 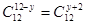из этого следует, что

12-у=у+2. у=5. Ответ: (12;5).

 

9.1. Решить систему уравнений:

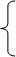а) = б) =

=153 =20

10. Решить уравнения:

а) =42х; б); в) ; г)

Лекция 3. Основные понятия теории графов


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)