Ориентированные графы

В ориентированных графах на рёбрах задано направление, т.е. у каждого ребра фиксируется начало и конец. Такие направленные рёбра называются дугами.

Цепью в ориентированном графе называется такая последовательность дуг, ведущих от вершины Р₁ к вершине Р _n, в которой каждые две соседние дуги имеют общую вершину и никакая дуга не встречается более одного раза.

Если направление цепи совпадает с направлением всех принадлежащих ей дуг, то цепь называется путём.

В ориентированных графах циклом называется путь, начало и конец которого совпадают. На рис. 3.12 дуги (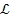 _{1, 4, 5}) образуют цепь, а дуги (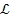 _{1, 2, 5}) – путь. Последовательность дуг (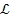 _{1, 2, 3}) составляет цикл, а последовательность (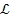 _{1, 2, 4}) не является циклом.

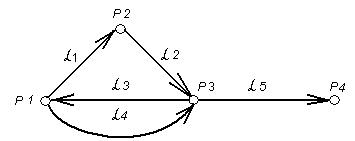
Рис. 3.12

Цепь, путь и цикл в произвольном графе называются простыми, если они не проходят ни через одну свою вершину более одного раза. Длинной цепи, пути, цикла называется число содержащихся в нём дуг.

Сетью называется граф, каждой дуги которого поставлено в соответствии некоторое число (или несколько чисел).

Многие практические задачи могут быть решены с помощью теории графов.

Поиск по сайту: