 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Операции над множествами
 Пересечением множеств A и В называют множество, состоящее из тех и только из тех элементов, которые одновременно принадлежат множествам A и В. Обозначают пересечение
Пересечением множеств A и В называют множество, состоящее из тех и только из тех элементов, которые одновременно принадлежат множествам A и В. Обозначают пересечение  , где
, где 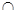 - символ пересечения.
- символ пересечения.
 ={ x x
={ x x  и x
и x  }
}
Пересечение множеств определяется конъюнкций высказываний, отсюда сходство знаков 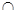 и
и  . Если
. Если  не пересекаются, пишут
не пересекаются, пишут  = Ø (рис. 1.4)
= Ø (рис. 1.4)

 = Ø
= Ø
рис. 1.4
Если же множества A и В имеют хотя бы один общий элемент, то они пересекаются и 
 Ø (рис. 1.5)
Ø (рис. 1.5)


 Ø
Ø
Рис. 1.5
 Заштрихованная площадь здесь - пересечение
Заштрихованная площадь здесь - пересечение  .
.
Объединением (суммой) двух множеств A и В называют множество  , состоящее из элементов, принадлежащих хотя бы одному из этих множеств.
, состоящее из элементов, принадлежащих хотя бы одному из этих множеств.
 С=А+В=
С=А+В=  ={ x x
={ x x  A
A  }={ x x
}={ x x  A или
A или  }- дизъюнкции высказываний.
}- дизъюнкции высказываний.
Объединение  изображается так:
изображается так:

Рис. 1.6
Понятия объединения и пересечения могут быть обобщены на случай любого числа множеств (конечного или бесконечного). Если даны множества А1, А2,... Ак,..., то символическая запись  означает объединение данных множеств, т.е. определяет множество, каждый элемент которого принадлежит хотя бы одному из Ак.
означает объединение данных множеств, т.е. определяет множество, каждый элемент которого принадлежит хотя бы одному из Ак.
Символическая запись  означает пересечение данных множеств, т.е. определяет множество, каждый элемент которого принадлежит всем данным множествам.
означает пересечение данных множеств, т.е. определяет множество, каждый элемент которого принадлежит всем данным множествам.
Пример: Найти пересечение и объединение множеств А и В, если А = {1;2;3;4;5}, B = {4;5;6;7}. В пересечение множеств А В войдут общие элементы: А 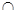 В = {4;5}. Объединение А В = {1;2;3;4;5;6;7} получается добавлением к элементам множества А недостающих элементов из множества В.
В = {4;5}. Объединение А В = {1;2;3;4;5;6;7} получается добавлением к элементам множества А недостающих элементов из множества В.
 Разностью множеств А и В называют множество А\В тех элементов множества А, которые не содержатся в множестве В:
Разностью множеств А и В называют множество А\В тех элементов множества А, которые не содержатся в множестве В:
С = А\В = { x x є A и x B }.
Если В  А, то разность А\В называют дополнением множества В до множества А и обозначают САВ или
А, то разность А\В называют дополнением множества В до множества А и обозначают САВ или  А. На диаграмме это обозначается так:
А. На диаграмме это обозначается так:

Рис. 1.7.
Если множества А и В пересекаются, то говорят об их разностях А \ В и В \ А. Изобразим разности на диаграммах Эйлера – Венна (Рис. 1.8).
А В

А\В В\А
Рис. 1.8
Свойства операций над множествами:
1. А  Ø = А.
Ø = А.
2. А  Ø = Ø.
Ø = Ø.
3.  А
А  А = А;
А = А;
(Идемпотентность)
А  А = А
А = А
4.  А
А  В = В
В = В  А;
А;
(Коммутативность)
А  В = В
В = В 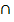 А
А
5.  А
А  (В
(В  С) = (А
С) = (А  B)
B)  С;
С;
(Ассоциативность)
А  (В
(В  С) = (А
С) = (А  В)
В)  С
С
6.  А
А  (В
(В  С) = (А
С) = (А  В)
В)  (А
(А  С);
С);
(Дистрибутивность)
А  (В
(В  С) = (А
С) = (А  В)
В)  (А
(А  С)
С)
7. Если А  Е и В
Е и В  Е, то:
Е, то:
 а) СЕ (А
а) СЕ (А  В) = СЕ А
В) = СЕ А  СЕ В, или
СЕ В, или
Е \ (А  В) = (Е \ А)
В) = (Е \ А)  (Е \ В);
(Е \ В);
(Законы двойственности)
б) СЕ (А  В) = СЕ А
В) = СЕ А  СЕ В, или
СЕ В, или
Е \ (А  В) = (Е \ А)
В) = (Е \ А)  (Е \ В)
(Е \ В)
8. Если В  А, то А
А, то А  В = А и А
В = А и А  В = В.
В = В.
Также как и конъюнкция, считается, что операция пересечения более «сильная», чем объединение, поэтому возможна запись
(А  В)
В)  С = А
С = А  В
В  С
С
(А  В)
В)  (А
(А  С) = А
С) = А  В
В  А
А  С.
С.
 Декартовым произведением множеств А и В называют множество А
Декартовым произведением множеств А и В называют множество А  В всех упорядоченных пар элементов (а, в) где а є А, в є В. Элементы а и в называют при этом компонентами (координатами) пары (а, в). Так, для произведения множеств X и Y используется запись X
В всех упорядоченных пар элементов (а, в) где а є А, в є В. Элементы а и в называют при этом компонентами (координатами) пары (а, в). Так, для произведения множеств X и Y используется запись X  Y = {(x; y) x є X
Y = {(x; y) x є X  y є Y }.
y є Y }.
Если множества X и Y совпадают, то говорят о декартовом произведении множества X само на себя:
X  Y = {(x; y) I x є X
Y = {(x; y) I x є X  y є X }.
y є X }.
Пусть заданы множества X = {1; 2; 3}, Y = { a; в }.
Тогда X  Y = {(1; а); (1; в); (2; а);(2; в); (3; а); (3; в)},
Y = {(1; а); (1; в); (2; а);(2; в); (3; а); (3; в)},
X  X = {(1;1);(1;2); (1;3); (2;1); (2;2); (2;3); (3;1); (3;2); (3;3)}.
X = {(1;1);(1;2); (1;3); (2;1); (2;2); (2;3); (3;1); (3;2); (3;3)}.
Элементы декартова произведения двух множеств можно также представить в виде таблицы или в виде графика.
Пример. Дано: X = { 1, 2, 3, 4 }
Y = { 4;5 }
Изобразить X  Y графиком на плоскости.
Y графиком на плоскости.
Решение. Множество X  Y состоит из следующих пар:
Y состоит из следующих пар:
А  В = {(1;4); (1; 5); (2;4); (2;5); (3;4); (3;5); (4;4); (4;5)}.
В = {(1;4); (1; 5); (2;4); (2;5); (3;4); (3;5); (4;4); (4;5)}.
Отметим эти точки на плоскости (Рис. 1.9)
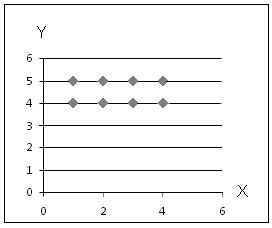
Рис. 1.9
Свойство декартового произведения:
1. X  Ø = Ø
Ø = Ø  X = Ø
X = Ø
2. X  Y ≠ Y
Y ≠ Y  X
X
3. X  (Y
(Y  Z) ≠ (X
Z) ≠ (X  Y)
Y)  Z
Z
4. X  (Y
(Y  Z) = X
Z) = X  Y
Y  (X
(X  Z)
Z)
5. X  (Y
(Y  Z) = (X
Z) = (X  Y)
Y)  (X
(X  Z)
Z)
Более общее определение произведения множеств X1, X2,X3,…,Xn:
 Декартовым произведением X1
Декартовым произведением X1  X2
X2  X3
X3  …
…  Xn называется множество, состоящее из упорядоченных n элементов, первая компонента которых принадлежит множеству X1, вторая – множеству X2, n -я -множеству Xn, т.е.
Xn называется множество, состоящее из упорядоченных n элементов, первая компонента которых принадлежит множеству X1, вторая – множеству X2, n -я -множеству Xn, т.е.
X1  X2
X2  …Xn = {(X1; X2;…;Xn) x1 є X1; x2 є X2; xn є Xn }
…Xn = {(X1; X2;…;Xn) x1 є X1; x2 є X2; xn є Xn }
Упорядоченная n -ка («энка») элементов, выбранных из множеств X1, X2,X3,…,Xn, называется КОРТЕЖЕМ (с фр. – торжественное шествие). Число n называют длиной кортежа, а элементы x1, x2, x3,…, xn – его компонентами.
Два кортежа (x1, x2,x3,…,xn) и (y1, y2,y3,…,ym) называют равными, если они имеют равные длины n = m и состоят из одних и тех же элементов, т.е. x1 = y1, x2 = y2,…, xn = ym
Количество элементов в декартовом произведении трёх множеств:
n (X1  X2
X2  X3 ) = n1 (X1)
X3 ) = n1 (X1)  n2 (X2)
n2 (X2)  n3 (X3)
n3 (X3)
Пример: Найти декартово произведение множеств
X1 = { a; в }, X2 = { 1;2 }, X3 = { 3;4;5 }
Решение:
X1  X2
X2  X3={(a;1;3),(a;1;4), (a;1;5) (a;2;3), (a;2;4), (a;2;5), (в;1;3), (в;1;4), (в;1;5), (в;2;3), (в;2;4), (в;2;5)
X3={(a;1;3),(a;1;4), (a;1;5) (a;2;3), (a;2;4), (a;2;5), (в;1;3), (в;1;4), (в;1;5), (в;2;3), (в;2;4), (в;2;5)
Количество элементов: n1  n2
n2  n3 =2
n3 =2  2
2  3= 12.
3= 12.
Поиск по сайту: