Определения и теоремы

Граф G – это совокупность двух конечных множеств: множества точек, которые называются вершинами, и множества пар вершин, которые называются рёбрами. На рис 3.1 изображен граф, имеющий пять вершин и шесть рёбер.

Рис.3.1

Если рассматривается множество упорядоченных пар точек, т.е. на каждом ребре задаётся направление, то граф G называется ориентированным. В противном случае граф G называется неориентированным.

Рёбра, имеющие одинаковые концевые вершины, называются парал–лельными. Ребро, концевые вершины которого совпадают, называются петлей.

На рис 3.1 - параллельные рёбра, а - петля.

Вершина и ребро называются инцидентными друг другу, если вершина является для этого ребра концевой точкой. На рис 3.1 вершина Р ₃ и ребро инцидентны друг другу.

Две вершины, являющиеся концевыми для некоторого ребра, называются смежными вершинами. Два ребра, инцидентные одной и той же вершине, называются смежными рёбрами. На рис 3.1 Р₁,Р₂ - смежные вершины, а - смежными ребрами.

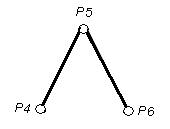
Степенью вершины называется число рёбер, инцидентных ей. Вершина степени 1 называется висячей, а вершина степени 0 – изолированной. На рисунке 3.1степень вершины Р ₁ равна трем, Р ₄ - висячая вершина, а Р ₅ – изолированная.

ТЕОРЕМА. В графе G сумма степеней всех его вершин – число чётное, равное удвоенному числу рёбер графа:

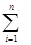степ.Р i = 2m (1)

где n – число вершин графа, а m – число его ребер. ТЕОРЕМА. Число нечётных вершин любого графа, т.е. вершин, имеющих нечётную степень, чётно.

Граф G называется полным, если любые две его различные вершины соединены ребром и он не содержит параллельных рёбер.

Дополнением графа G называется граф с теми же вершинами, что и граф G, и содержащий только те рёбра, которые нужно добавить в графу G, что- бы получился полный граф.

На рисунке 3.2 изображены следующие графы: G ₁- полный граф с пятью вершинами; G ₂ – некоторый граф, имеющий пять вершин; ₂ – дополнение графа G₂.

G ₁ G _{2 2}

Рис. 3.2

Путём в графе называется такая последовательность рёбер, ведущая от некоторой начальной вершины Р ₁ в конечную вершину Р_n, в которой каждые два соседних ребра имеют общую вершину и никакое ребро ни встречается более одного раза. Например, в графе, изображенном на рис. 3.1последователь- ность рёбер образует путь, ведущий от вершины Р ₁ к вершине Р ₄.

Циклом называется путь, начальная и конечная вершины которого совпадают. На рис 3.1 рёбра образуют цикл. Цикл графа G называется простым, если он не проходит ни через одну вершину G более одного раза.

Длиной пути (или цикла) называется число рёбер этого пути (или цикла).

Граф G называется связным, если для любых его вершин существует путь, их соединяющий. В противном случае граф G называется несвязным.

Любой несвязный граф является совокупностью связных графов. Эти связные графы обладают тем свойством, что никакая вершина одного из них не связана путём ни с какой вершины другого. Каждый из этих графов называется компонентой графа G. На рис. 3.3 изображен несвязный граф G с компонентами G₁,G₂,G₃. Каждая компонента является связным графом.

G₁ G₂ G₃

Рис 3.3

ТЕОРЕМА. Для того, что бы граф G представлял собой цикл, необходимо и достаточно, что бы каждая его вершина имела степень 2.

Ребро £ называется мостом графа G, если граф, получившийся из G после удаления ребра £ (такой граф обозначается G\£), содержит больше компонент, чем граф G.

ТЕОРЕМА. Ребро £ графа G является мостом тогда и только тогда, когда £ не принадлежит ни одному циклу.

Поиск по сайту: