Бинарные соответствия между множествами

Дадим определение бинарному соответствию между элементами множества X и Y (слово «бинарный» происходит от латинского BIS - дважды).

Бинарным соответствием называют тройку множеств. Множество X, множество Y и некоторое подмножество G их декартового произведения X Y. Множество X называют множеством отправления соответствия, множество Y - множеством прибытия соответствия, множество G 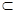X *Y - графиком соответствия.

Например: X – множество всех поездов, отправляющихся со станции Челябинск, Y – множество всех конечных станций прибытия, G - множество всех железнодорожных маршрутов со станции г. Челябинска. Таким образом, бинарное соответствие можно представить в виде ориентированного графа с множеством рёбер G. Чаще соответствие задается некоторым двухместным предикатом – предложением, содержащим переменную (например уравнения, неравенства и т.д.).

Двухместный предикат обозначается R(x; y), где x X, а y Y: поезд

x следует до станции y. Для бинарных соответствий двухместный предикат

R(x; y) записывается xRy и читается: элемент x находится с элементом y в отношении R.

Например, таблица 1 задает отношение «Группа x сдает экзамен в день y»

Поиск по сайту: