 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Правило произведения
Правило произведения касается числа кортежей, которые можно составить из элементов данных конечных множеств. Количество элементов в декартовом произведении n (Х 
Y) = n (X) n (Y) (4)
(смотрите лекцию 1 п. 1.4), n (X1 X2 … Xn) = n (X1) n (X 2) … n (Xn) (5)
В комбинаторике равенство (4) обычно формулируют следующим образом. Если элемент х можно выбрать n способами, а элемент y – m способами, то упорядоченную пару (х;y)можно выбрать n m способами.
Пример 1 Из деревни А в деревню В ведут три дороги, а из В в С – две дороги. Сколькими способами можно пройти из деревни А в деревню С через деревню В?
Решение: Обозначим дороги из А в В числами 1,2и 3, а из В в С буквами a,в. Тогда каждый вариант пути из А в С задаётся парой из числа и буквы, т.е. (1 а),(2 a),(3 a), (1 в),(2 в),(3 в) (Рис 2.3).
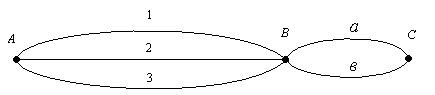
Рис 2.3
Число пар можно найти и по правилу произведения:3 2=6.
Пример 2 Набор составляется из авторучки и открытки. Сколько различных наборов можно составить, имея 5 различных авторучек и 14 различных открыток?
Решение: В задаче речь идёт о выборе пары (авторучка, открытка), осуществить его можно 5 14=70 способами. Следовательно, из 5 различных авторучек и 14 различных открыток можно составить 70 наборов.
Поиск по сайту: