 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
А. Базовое системное соотношение
На основе приведенной выше методики число входных (Nцвхi) и выходных (Nцвыхi) цепей в логической схеме на i ‑м уровне компоновки можно представить выражениями:
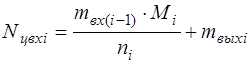(3.14)
(3.15)
а с учетом условия Nцвхi = Nцвыхi и ряда простых преобразований имеет место соотношение:
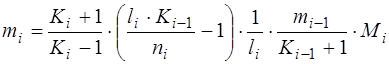(3.16)
Приведенное выражение (3.16) является промежуточным видом базового системного соотношения, характеризующего фундаментальную взаимосвязь основных компоновочных параметров в логической схеме устройства.
Входящий в (3.16) множитель 
может быть заменен на другой, учитывающий покаскадное изменение числа выходных логических цепей при распространении информационного сигнала в логической схеме от входа до ее выхода. В частности, это изменение можно представить аналитическим выражением:
, (3.17)
откуда получено, так называемое, “ключевое соотношение”:
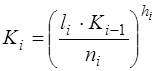(3.18)
Выражение (3.18) играет особо важную (“ключевую”) роль во взаимосвязи части системы компоновочных параметров логической схемы, где учитываются параметры цепей по нагрузочной способности (ni и li), число каскадов элементов hi и связь уровней компоновки устройства посредством параметров Ki‑ 1 и Ki.
Использование ключевого соотношения (3.18) позволяет преобразовать промежуточный вид системного соотношения (3.16) в новый, более упрощенный вид, а именно:
(3.19)
Формула (3.19) представляет собой итоговое аналитическое выражение базового системного соотношения статической модели, устанавливающее фундаментальную взаимосвязь основных компоновочных параметров в логической схеме устройства на любом (i ‑м) уровне компоновки.
Примечание
Базовое системное соотношение, полностью идентичное по форме аналитическому выражению (3.19), может быть получено и другим путем, в частности, в результате анализа покаскадного и суммарного числа элементов в ФП логической схемы устройства, т.е.
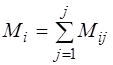, (3.20)
где Mij ‑ число элементов в j ‑м каскаде модели ФП логической схемы устройства на i ‑м уровне компоновки, которое может быть выражено как с помощью входных контактов элементов (mвхij), так и с помощью выходных (mвыхij), используя параметры цепей по нагрузочной способности по входу (ni) и выходу (li), т.е.:
; 
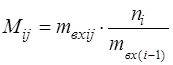. (3.21) (3.22)
В результате использования (3.17) и (3.22) число элементов в j ‑м каскаде определится как:
, (3.23)
при этом общее число элементов Mi в соответствии с (3.20) определится с помощью выражения:
,
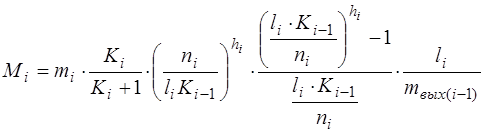откуда:
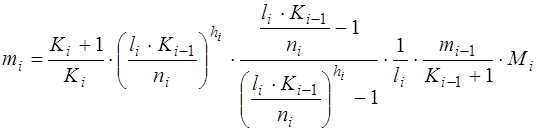. (3.24)
Выражение (3.24) представляет собой другой промежуточный вид базового системного соотношения, характеризующего фундаментальную взаимосвязь основных компоновочных параметров в статической модели ФП логической схемы устройства.
С учетом ключевого соотношения (3.18) и ряда преобразований в (3.24), можно получить полностью адекватное аналитическое выражение базового системного соотношения, приведенного в (3.19).
Поиск по сайту: