 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Принципы, критерии и законы системной взаимосвязи при матричных (классических) методах компоновки
Параметр ri, представляющий собой главный вектор модели логической схемы, играет определяющую роль при практическом применении системных соотношений. От законов изменения этого параметра зависят значения практически всех параметров логической схемы и их достоверность.
Главными факторами в матричных (классических) методах компоновки, влияющими на изменение параметра ri, являются функциональный объем и используемые принципы компоновки элементов на структурных уровнях. Эти факторы в определенной мере связаны друг с другом, однако их влияние можно рассматривать и раздельно.
Зависимость параметра ri от функционального объема (первый фактор) характеризуется особенностью, которая заключается в том, что ее целесообразно определять через взаимосвязь с параметром Ki, который с функциональным объемом Mi, согласно базового критерия (4.1), находится в полном соответствии. Изменение параметров ri и Ki по отношению друг к другу происходит по принципу “противофазности” изменения их значений, т.е. если с увеличением функционального объема значение Ki уменьшается, то одновременно значение ri соответственно увеличивается.
Использование данного принципа позволяет представить взаимосвязь параметров ri и Ki в виде критерия взаимосвязи, характеризуемого суммой их значений и постоянством величины этой суммы на каждом уровне компоновки устройства, т.е.:
 , (4.3)
, (4.3)
откуда зависимость параметра ri от функционального объема (через взаимосвязь с параметром Кi) в общем случае имеет вид:
 . (4.4)
. (4.4)
Вместе с тем, на эту взаимосвязь накладывают отпечаток используемые в схемах принципы компоновки элементов (второй фактор). На каждом отдельном уровне может быть реализован только один принцип построения (объединения) элементов схемы, которому соответствует только одно значение постоянной величины Аi. Но так как логическая схема может содержать несколько структурных уровней (i ‑уровней компоновки), то принципов построения также может быть несколько (в общем случае от 1‑го до i) и каждому из них будет соответствовать свое значение постоянной величины Аi, определяемое начальными условиями компоновки элементов на каждом уровне, т.е. при Mi ’ = 1.
Максимальное значение этой постоянной величины (А max), определяемое начальным условием компоновки на 1‑м уровне (т.е. когда Mi ’ = 1 ЭЛЭ, Ki ’ = K 0, ri ’ = r 0 = 1, составляет:
 . (4.5)
. (4.5)
Если принцип компоновки элементов на последующих уровнях не меняется, то это начальное условие остается справедливым и для других структурных уровней (а значит и для всей схемы в целом), что можно представить выражением:
 , (4.6)
, (4.6)
откуда зависимость параметра ri от функционального объема (через Кi при едином принципе компоновки элементов в устройстве определится соотношением:
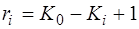 . (4.7)
. (4.7)
Если принцип компоновки элементов на каждом последующем уровне постоянно меняется, то меняются всякий раз и начальные условия, определяемые значениями параметров: Mi ’ = 1; Ki ’ = Ki -1; ri ’ = r 0 = 1, в результате чего максимальное значение постоянной (в пределах каждого уровня) величины A max i для такого случая можно представить новым выражением:
 , (4.8)
, (4.8)
откуда зависимость параметра ri от функционального объема (через параметр Кi) для случая постоянно меняющегося принципа компоновки элементов на каждом структурном уровне схемы определяется соотношением:
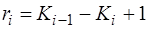 . (4.9)
. (4.9)
Приведенные соотношения (4.7) и (4.9) представляют собой два основных закона изменения параметра ri в компоновочной модели логической схемы устройства: первый – когда в устройстве на всех структурных уровнях используется только один принцип компоновки элементов, второй – когда на всех структурных уровнях устройства используются разные принципы компоновки элементов.
Вместе с тем, в обрабатывающих устройствах ЭВМ могут иметь место и их сочетания. Возможные варианты принципов компоновки устройства по уровням и соответствующие им значения постоянной величины Аi, а также возможные варианты их сочетаний приведены в таблице 4.1, а графическое их представление – на рис. 4.2.
Таблица 4.1
| Варианты сочетания принципов компоновки в устройстве и законов изменения параметра ri | Возможные варианты принципов компоновки устройства по уровням и соответствующие им значения постоянной величины Вi (Вi = Ki × ri) | |||||
| i = 1 | i = 2 | i = 3 | i = 4 | … | i = i | |
| K 0 | K 0 | K 0 | K 0 | … | K 0 | |
| K 0 | K 1 | K 1 | K 1 | … | K 1 | |
| K 0 | K 1 | K 2 | K 2 | … | K 2 | |
| K 0 | K 1 | K 2 | K 3 | … | K 3 | |
| … | … | … | … | … | … | … |
| i | K 0 | K 1 | K 2 | K 3 | … | Ki -1 |
Примечание
Взаимосвязь параметров ri и Ki можно представить и другим, близким по смыслу, критерием взаимосвязи, характеризуемым не суммой, а произведением значений параметров ri и Ki и постоянством этого произведения на каждом уровне компоновки устройства, т.е.:
 . (4.10)
. (4.10)
В этом случае законы изменения параметра ri определяются выражениями:
– 1‑й закон, отражающий использование единого принципа компоновки элементов на всех уровнях устройства:
 . (4.11)
. (4.11)
– 2‑й закон, отражающий использование разных принципов компоновки на каждом уровне устройства:
 . (4.12)
. (4.12)
Результаты практических расчетов компоновочных параметров логической схемы при использовании законов, полученных как на основе данного критерия, так и на основе вышеприведенного, близки и сравнимы между собой.

Рис. 4.2. Графическое представление возможных вариантов принципов компоновки устройства по уровням и соответствующие им значения величины Вi.
Отличительной особенностью приведенных законов является вид зависимости ri от функционального объема устройства, выраженного степенью интеграции (т.е. числом ЭЛЭ). Если при 1‑м основном законе (ri = K 0 – Ki + 1) эта зависимость характеризуется непрерывностью изменения ri на всем диапазоне степени интеграции устройства, то при 2‑м основном законе (ri = Ki ‑1 ‑ Ki + 1) она характеризуется ступенчатостью изменения параметра ri при переходе от одного уровня компоновки к другому. При этом максимальное значение параметра ri постепенно снижается и в пределе (при Ki = 1) приближается к 1, т.е. ri = Ki ‑1 ® 1 (в отличие от 1‑го закона, где ri = K 0 >> 1). Графическое представление законов изменения параметра ri с ростом степени интеграции приведено на рис. 4.3.

Рис. 4.3. Графическое представление законов изменения параметра ri с ростом степени интеграции Ni.
Приведенные законы изменения параметра ri являются отражением используемых принципов компоновки элементов как на отдельных уровнях, так и в устройстве в целом. Проведенные исследования [1] показывают, что 1‑му закону изменения параметра ri в полной мере соответствует единый (в пределах трех уровней) принцип компоновки элементов и устройств, используемый в ИС (i = 1), ТЭЗах (i = 2) и панелях (i = 3) ЕС ЭВМ 3‑го поколения (а также других аналогичных систем ЭВМ), характеризующихся централизованной системой управления. В дальнейшем этот принцип будем именовать как “ общепроцессорный ” принцип компоновки элементов в логической схеме устройства.
2‑му закону изменения параметра ri соответствуют (в пределах младших уровней, i = 1…4) принципы компоновки элементов и устройств, используемые в микропроцессорах (i = 1, 2) и устройствах на их основе (i = 3, 4), характеризующихся, как правило, распределенной системой управления. В дальнейшем эти принципы интегрально будем именовать как “ микропроцессорный ” принцип компоновки элементов в логической схеме устройства.
Целесообразно здесь также отметить, что для конструктора главными внешними признаками процессорного и микропроцессорного принципов компоновки и законов их описывающих являются характеристики по числу внешних контактов в элементах и устройствах и быстродействию, выражаемому числом каскадов ЛЭ. Если для процессорного принципа (в соответствии с 1‑м законом изменения ri) характерно максимальное число внешних контактов и высокое быстродействие, то для микропроцессорного принципа (в соответствии со 2‑м законом) характерно минимальное число внешних контактов и более низкое быстродействие.
Примечание
Микропроцессоры и микропроцессорные устройства характеризуются, как правило, наличием внутренней памяти (ЗУ). Эта память может быть выполнена в двух основных вариантах: либо совместно с комбинационной частью и входить в состав кристалла БИС, либо в виде отдельного кристалла ЗУ. Расчет числа внешних контактов в таких устройствах при использовании системных соотношений и приведенных законов не учитывает совместного использования ЗУ и связанного с ним числа внешних цепей. Поэтому получаемое в результате расчета число внешних контактов (напр., для микропроцессора, содержащего ЗУ) будет больше на то число цепей, которое связывает ЗУ с комбинационной частью.
Поиск по сайту: