Системные соотношения динамической модели

Представленный выше вариант базового системного соотношения (3.29) характеризует взаимосвязь основных компоновочных параметров логической схемы применительно к статической модели. В такой модели схемы число элементов в одном каскаде M_i /h_i является важным параметром, однако значение его является неопределенным, несмотря на то, что значение числа элементов M_i, как правило, является заданным. Нахождение значение параметра M_i /h_i лежит в плоскости использования динамической модели логической схемы.

Как уже отмечалось ранее (см. 3.2.1), динамическая модель, в отличие от статической, кроме основных компоновочных параметров, характеризуется рядом взаимосвязанных динамических параметров, к которым, главным образом, относятся вектор модели ФП элементов r_i и вектор модели ФП выходных логических цепей r_i^l. Применение указанных векторов позволяет характеризовать модели ФП элементов и логических цепей на каждом уровне компоновки рядом частных соотношений модели (см. 3.2.1), использование которых в вариантах базового системного соотношения с измененным основным аргументом преобразует статическую модель логической схемы в динамическую, восстанавливая одновременно основной аргумент в функции m_i, выраженный числом элементов M_i.

Таким образом, с учетом дополнительных параметров и используя частные соотношения динамической модели, аналитическое выражение фундаментальной взаимосвязи компоновочных параметров в логической схеме устройства представлено следующими конечными видами системных соотношений:

(3.30)

или

, (3.31)

где

; .

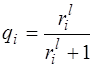Примечание

Приведенные выше системные соотношения для динамической модели логической схемы по своей форме во многом напоминают правило Рента (с учетом некоторых условий) и могут быть использованы для определения физического смысла коэффициентов “ a ” и “ b ” как в самом правиле, так и соотношениях Рента. Так, например, для 1‑го уровня компоновки (i = 1; M ₁ = N ₁) и при условии l_{i= 1} = 1 (или, что то же самое, q_{i= 1} = 0) системное соотношение, с учетом того, что m_o /K_o + 1) = 1, имеет вид:

(3.32)

Это значит, что применительно к правилу Рента можно однозначно определить физический смысл коэффициентов a и b, значения которых не являются постоянными с ростом степени интеграции и определяются выражениями:

,

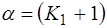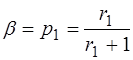
При изменении параметров K ₁ и r ₁ в диапазоне, напр., от K ₁ = 3 до K ₁ = 1 и от r ₁ = 1 до r ₁ = 3, диапазоны значений коэффициентов a и b составляют: a = 4…2; b = 0,5…0,75, что в целом соответствует известным соотношениям Рента.

Из приведенного краткого анализа правила и соотношений Рента на основе использования системных соотношений динамической модели можно сделать следующие важные выводы:

1. Коэффициенты a и b в соотношениях Рента не есть константы (что часто так трактуется в публикациях), а являются переменными величинами, значения которых могут быть определены только при известных законах изменения параметров “ K ” и “ r ”;

2. Нельзя использовать в соотношениях Рента средние значения коэффициентов a и b из соответствующих диапазонов, т.к. большему значению a, как правило, соответствует меньшее значение b и наоборот;

3. В соотношениях Рента не учитываются нагрузочные способности логических цепей по выходу (q = 0, а значит l = 1 = Const), что существенно влияет на число внешних контактов и значения других компоновочных параметров;

4. Соотношения Рента не могут распространяться на другие уровни компоновки, кроме первого, т.к. на других уровнях значение величины m_{i‑ 1}/(K_{i‑ 1} + 1) >> 1, а значит a_{i‑ 1} >> a_i. Кроме того, законы изменения параметров r на других уровнях компоновки могут существенно отличаться от аналогичных законов, присущих для 1‑го уровня.

Поиск по сайту: