Исходные соотношения. Правило Рента

* Эмпирическое соотношение Рента (правило Рента).

В течение длительного времени (с начала 60‑х годов и практически по настоящее время) в качестве основного вида взаимосвязи между параметрами элементов и устройств ЭВМ использовалось известное широкому кругу специалистов “Правило Рента”. Это правило, полученное экспериментальным путем, устанавливает упрощенную эмпирическую взаимосвязь между двумя компоновочными параметрами логической схемы устройства, а именно между числом внешних контактов (m) и степенью интеграции (N), и выражается эмпирической зависимостью в виде степенной функции вида:

, (3.1)

где a и b есть некоторые коэффициенты.

На основе этого правила создано большое число эмпирических соотношений Рента, в которых коэффициенты a и b находятся в широком диапазоне значений. В большинстве случаев такой диапазон значений обычно составляет [9]: a = 3…5; b = 0,5…0,75.

Главным достоинством правила и соотношений Рента является их простота и удобство применения при оценке числа внешних связей в элементах и устройствах ЭВМ. Эта простота позволяла в 60 – 70‑х годах использовать соотношения Рента как при определении числа внешних связей, так и при выборе других параметров конструкции устройств, напр., при оценке средней длины связи, определении конструктивной задержки и др.

Главным же недостатком соотношений Рента при конструировании современных устройств ЭВМ является недопустимо широкий диапазон значений числа внешних контактов, обусловленный отсутствием унифицированной единицы измерения степени интеграции (т.е. характеристик ЛЭ, через который оценивается степень интеграции N) и неопределенностью физического смысла коэффициентов a и b.

Вместе с тем, длительная неопределенность в определении физического смысла коэффициентов a и b, и их возможная зависимость от других параметров существенно ограничивали возможности практического применения соотношений Рента. Поэтому в разные годы авторами различных публикаций предлагались периодически меняющиеся диапазоны значений коэффициентов в соотношениях Рента. Приведенные выше диапазоны значений в большей степени характерны для периода 60‑х и 70‑х годов. В 80‑е годы большей популярностью пользовались диапазоны значений, составляющие: a = 2,5…3,5 и b = 0,5…0,75 [6]. Существенно претерпели они в конце 80‑х: a = 1,3…4,5 и b = 0,4…0,6 [10].

Однако наибольшие изменения в значениях коэффициентов a и b отражены в зарубежных публикациях начала 90‑х годов, которые рассматриваются принципиально в другой плоскости, в частности, в зависимости от типа логики в схеме устройства (микропроцессор, МаБИС, произвольная логика), архитектуры ЭВМ и методов обработки информации в устройствах (высокопроизводительные ЭВМ, ЭВМ с параллельной, матричной и конвейерной обработкой) и в общей сложности вписываются в огромные диапазоны значений, а именно [11]:

a = 0,005…82 и b = 0,25…0,92

Таким образом, последние виды соотношений Рента, характеризующиеся значительно большим диапазоном значений коэффициентов a и b, также не раскрывают физического смысла последних и, по существу, исключают возможность практического применения широко известного и популярного в прошлом правила и соотношений Рента при проектировании современных быстродействующих и высокоинтегрированных средств ВТ, использующих новые принципы построения устройств и методы обработки информации.

* Статистическое соотношение Микитина-Рента
(для ЕС ЭВМ).

Проблеме “правила и соотношений Рента” большое внимание уделено при разработке конструкций устройств старших моделей ЕС ЭВМ.

На основе статистического исследования параметров конструкций устройств младших моделей ЕС ЭВМ, проведенное Микитиным В.М. в 1980 г [12], получено экспериментальное (статистическое) соотношение, отражающее более достоверную взаимосвязь между числом внешних контактов и степенью интеграции устройств в широком диапазоне функционального объема: от 1‑го ЛЭ до объема панели в 10…30 тыс. ЛЭ. Это соотношение, известное как статистическое соотношение Микитина-Рента (для ЕС ЭВМ), имеет вид [12, 2]:

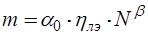, (3.2)

где:

a ₀ – фиксированное значение числа входов/выходов в ЭЛЭ, равное 4 (для 3‑х входового ЭЛЭ);

h_лэ – эффективность использования входов/выходов ЭЛЭ в схемах, составляющая примерно 0,9 (при a ₀ = 4);

b – показатель степени, определяемый степенной функцией вида:

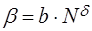, (3.2’)

где b = 0,38…0,42 и d = 0,04 – статистические коэффициенты.

Главным достоинством статистического соотношения является относительная простота и возможность получения более достоверных (в узких границах) значений числа внешних связей в конструкциях устройств. Однако, именно в силу своей простоты, данное соотношение ограничено областью своего применения (только в структурах ЭВМ 3‑го поколения, т.е. типа ЕС ЭВМ) и не учитывает методов и принципов компоновки элементов в устройствах ЭВМ и связанных с ними новых методов обработки информации.

* Аналитическое соотношение Файзулаева-Рента.

Впервые воздействовать на само “правило Рента”, попытка вывести его аналитически предпринята в 1987г. советским ученым Файзулаевым Б.Н. [13]. Главная суть предложения Файзулаева заключается в двух нововведениях: введено понятие “функциональное поле” логической схемы устройства и введен в “правило Рента” новый параметр “ Н_К ”, характеризующий быстродействие устройства.

Соотношение, полученное Файзулаевым и основанное на “правиле Рента”, именуемое как “аналитическое соотношение Файзулаева-Рента”, с учетом нововведений имеет вид:

(3.3)

где:

a – среднее число входов/выходов в ЛЭ;

H_К – средняя глубина логических цепей (т.е. число каскадов ЛЭ в логической схеме устройства).

b – показатель степени, определяемый степенной функцией вида:

Соотношение (3.3) может быть представлено в другой форме:

(3.3’)

где

(3.3”)

Отдавая дань первооткрывателю “правила Рента”, автор [13] предложил именовать показатель степени “ p ” как “показатель Рента”.

Главными “стратегическими” недостатками всех соотношений Рента являются:

– ограниченность по количеству и отсутствие ряда важных компоновочных параметров в соотношениях (напр., параметров по нагрузочной способности логических цепей и др.);

– отсутствие четко выраженной единицы измерения функционального объема устройств, что существенно снижает достоверность результатов расчета параметров;

– отсутствие параметров, характеризующих границы и условия применения соотношений, напр., границ вычислительного процесса, связанного с обработкой информации, условий функциональной законченности (завершенности) обрабатывающего устройства ЭВМ и др.

– отсутствие параметров и критериев, отражающих методы и принципы компоновки современных устройств по всем структурным уровням ЭВМ.

Этих недостатков лишены соотношения, характеризующиеся системной взаимосвязью компоновочных параметров в устройствах.

Поиск по сайту: