Характеристики розподілу вибіркових даних

Задача математичної статистики полягає в створенні методів збору та обробки статистичних даних для одержання наукових і практичних висновків.

Вся сукупність об’єктів, що підлягає вивченню, називається генеральною сукупністю.

Та частина об’єктів, що потрапила на перевірку, називається вибірковою сукупністю або вибіркою. Число елементів сукупності називається її об’ємом. Значення кількісної ознаки , що спостерігаються, називаються варіантами. Послідовність варіант, записаних у зростаючому порядку, називають варіаційним рядом. Число спостережень значення називається частотою варіанти . Відношення частоти до об’єму вибірки називається відносною частотою або частістю

.

Статистичним розподілом вибірки називають перелік варіант і відповідних їм частот або відносних частот.

			…
			…
			…

Емпіричною функцією розподілу називають функцію , що визначає для кожного значення 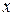відносну частоту події

,

– число спостережень, в яких сприймала значення ознака ,

менше, ніж ,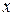

– загальне число спостережень (об’єм вибірки).

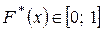– емпірична функція є аналогом інтегральної функції випадкової величини .

Полігоном частот називають ламану, відрізки якої з’єднують точки .

Полігоном відносних частот називають ламану, відрізки якої з’єднують точки .

У випадку неперервного статистичного розподілу будують гістограму. Гістограмою частот називають фігуру, що є сукупністю прямокутників, основи яких дорівнюють довжинам інтервалів , а висоти дорівнюють густині частоти (тобто відношенню ). Гістограма відносних частот будується відповідно до густини відносних частот. Площа гістограми відносних частот дорівнює одиниці. Це властивість ідентична властивості ймовірностей подій, що утворюють повну групу.

Накопичені частоти – це результати послідовного підсумовування частот усіх варіант (чи частот інтервалів), включаючи частоту даної варіанти (чи інтервалу). Накопичені частоти показують число членів сукупності, для яких ознака не перевищує даного значення. Кумулятивна крива – це ламана лінія, відрізки якої з’єднують точки .

Середні величини розглядаються в статистиці як узагальнюючі показники, у яких знаходять вираження дія загальних для даного явища умов. Основною середньою величиною є середнє арифметичне чи вибіркове середнє.

Вибірковим середнім називають середнє арифметичне значення ознаки вибіркової сукупності

.

Властивості вибіркового середнього:

1. .

2. , чи .

Медіана – це варіанта, яка знаходиться в середині варіаційного ряду.

Для дискретного варіаційного ряду:

Для інтервального варіаційного ряду:

			…
			…

,

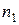
де – медіанний інтервал, що вибирають за серединним значенням,

– об’єм вибірки,

– частота медіанного інтервалу,

– сума частот інтервалів, які є попередніми до медіанного.

Модою називають значення варіанти, яка має найбільшу частоту.

Для дискретного варіаційного ряду мода визначається безпосередньо порівнянням частот.

Для інтервального варіаційного ряду

,

де – модальний інтервал з найбільшою частотою,

– частота модального інтервалу,

– частота інтервалу, який є попереднім до модального,

– частота інтервалу, який є наступним за модальним.

Показники варіації

Варіація індивідуальних значень ознаки є атрибутивною властивістю явища. В ній виражається вплив множини випадків, характерних для досліджуваного явища. Показники варіації разом із середніми величинами представляють той фундамент, на який спирається математико-статистичний аналіз.

Розмах варіації (або її амплітуда) – це різниця між найбільшим і найменшим значеннями варіант

.

Середнє абсолютне або середнє лінійне відхилення – це зважене частотами середнє з абсолютних відхилень варіант ряду від вибіркового середнього

.

Вибірковою дисперсією називають середнє арифметичне квадратів відхилень значень ознаки, що спостерігаються, від їх середнього значення

або

,

де .

Середнім квадратичним відхиленням називають корінь квадратний з дисперсії .

Лінійний коефіцієнт варіації – це відносна характеристика ступеня коливань ознаки

.

Коефіцієнт варіації служить для порівняння величин розсіювання двох варіаційних рядів: той з рядів має більшу варіацію, у якого коефіцієнт варіації більше.

Розв’язання. Об’єм вибірки .

Полігон частот має вигляд:

Емпірична функція розподілу

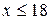
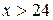
Вибіркове середнє:

.

Медіана:

– парне число,

, .

.

Знайдемо накопичені частоти

Починаючи з четвертої по дев’яту, варіанти мають значення 22. Отже, і .

.

Мода:

найбільша частота відповідає варіанті 22.

.

Розмах варіації:

.

Середнє абсолютне відхилення:

.

Вибіркова дисперсія:

,

.

Середнє квадратичне відхилення:

.

Коефіцієнт варіації:

.

	0 – 2	2 – 4	4 – 6	6 – 8	8 – 10	10 – 12

Полігон побудуємо по серединах інтервалів розподілу:

Знайдемо накопичені частоти:

	0 – 2	2 – 4	4 – 6	6 – 8	8 – 10	10 – 12

Медіана:

, .

(6; 8) – медіанний інтервал.

, .

, .

.

Мода:

найбільша частота визначає модальний інтервал (4; 6).

, .

, , .

.

Поиск по сайту: