Критерії згоди. Основні поняття

У попередніх прикладах закон розподілу вважався відомим, або існували досить вагомі підстави для припущення про форму закону розподілу по даному емпіричному матеріалу. Порівняння фактичних і обчислених теоретичних частот указує на їх близькість, але повної збіжності немає. Між і є визначені, іноді досить значні розбіжності. Відхилення фактичних частот від теоретичних можна пояснити за допомогою двох тверджень:

1. Емпіричні і теоретичні частоти не суперечать одна однієї, а розбіжності між ними необхідно вважати випадковими, оскільки вибір елементів дослідження проводили випадковим способом. Зроблене припущення про розподіл ознаки за теоретичним законом варто визнати вірним.

2. Розбіжності між теоретичними і емпіричними частотами пояснити випадковістю неможливо. Розподіл ознаки по обраному теоретичному закону необхідно визнати помилковим. Варто ретельніше вивчити варіаційний ряд і спробувати підібрати новий закон, що точніше враховував би особливості емпіричного матеріалу.

Для вибору між цими двома висновками застосовують критерії згоди.

Критерієм згоди називають правило перевірки гіпотези про припущений закон невідомого розподілу.

Розглянемо деякі з них.

Критерій згоди Пірсона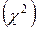

Припустимо, що у результаті спостережень за випадковою величиною отриманий її розподіл у виді варіаційного ряду, який характеризується частотами .

Їх сума – це об’єм сукупності . Припустимо, що емпіричним частотам відповідають теоретичні .

За міру розбіжності теоретичного і фактичного рядів частот Пірсон запропонував узяти середнє арифметичне квадратів відхилень відповідних частот, розділених на теоретичні частоти

(1)

Якщо всі фактичні і теоретичні частоти збігаються, то випадкова величина . В інших випадках величина (1) відрізняється від нуля, і тим більше, чим більше розбіжності між і . Із таблиці критичних значень Пірсона знаходять значення , де 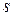– це число груп (часткових інтервалів) вибірки; – число параметрів теоретичного розподілу, що було оцінено за даними вибірки, – рівень значимості, що визначає величину припустимої помилки (0,1; 0,05; 0,01). У випадку нормального розподілу =2 (математичне сподівання і дисперсія), у випадку розподілу Пуассона =1 (оцінюють один параметр ).

Правило застосування критерію Пірсона:

1. обчислити величину за формулою (1);

2. знайти по таблиці

3. порівняти фактичне і критичне значення

а) – немає підстав для відхилення висунутої гіпотези про теоретичний закон розподілу;

б) – гіпотезу про закон розподілу варто відхилити.

Для перевірки правильності обчислень використовують формулу

.

Розв’язання:

Допоміжні обчислення зручно проводити в таблиці

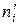
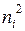
				0,06		20,06
				0,01		113,01
		-2		0,03		133,03
		-1		0,01		103,01
				0,02		52,02
				0,13		500,13

розподіл обраний вірно.

Емпіричні дані спостережень погоджені з гіпотезою про нормальний розподіл генеральної сукупності.

Поиск по сайту: