АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Припустимо, що у результаті випробування отримано інтервальний варіаційний ряд ознаки

Читайте также:
  1. IV. ПОВТОРНІ ВИПРОБУВАННЯ
  2. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  3. Акти застосування права: поняття, ознаки, види, структура
  4. Аналіз результатів учнів 8 класу на ІІІ етапі Всеукраїнської учнівської олімпіади з географії у Житомирській області 2014 року
  5. Аналіз фінансових результатів операційної діяльності
  6. Атрибутивні ознаки і властивості культури
  7. Врахування результатів екологічної оцінки при прийнятті рішень
  8. Г) обчислення й аналіз результатів.
  9. Держава як суб’єкт міжнародного приватного права. Імунітет держави: поняття, ознаки, види.
  10. ДЕРЖАВНІ ОРГАНИ: ЇХ ОЗНАКИ, ХАРАКТЕРИСТИКА І ВИДИ
  11. Дискретний варіаційний ряд часток
  12. Для знаходження середнього квадрата ознаки складемо таблицю

 

Значення показника …
Частоти …

,

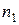
і дослідник має підстави вважати його розподіленим за нормальним законом. Для побудови нормального закону необхідно обчислити вибіркову середню і дисперсію цього розподілу. Відповідно до закону великих чисел вибіркова середня є оцінкою математичного сподівання , а дисперсія – оцінкою дисперсії нормального закону. Нормальний закон з параметрами і буде теоретичним законом, що відображає розподіл ознаки в генеральній сукупності.

 

Приклад. Зріст дорослих чоловіків є випадковою величиною, розподіленою за нормальним законом. Знайти загальні вирази густини ймовірності і функції розподілу за даними таблиці

 

168-170 170-172 172-174 174-176 176-178 178-180 180-182 182-184 184-186
                 

 

. Замінимо інтервали на їх середини

 

                 
                 

 

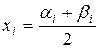
За формулами і обчислюємо вибіркову середню і дисперсію

.

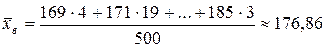
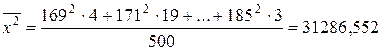
Тоді , , . Густина ймовірності

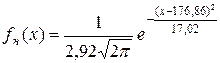
Функція розподілу має вигляд

 

 


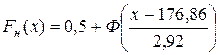
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)