Для знаходження середнього квадрата ознаки складемо таблицю

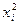
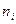
Тоді за формулою (12.7) заняття 12 знайдемо квадрат середньої

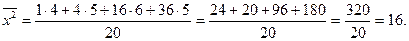
Враховуючи, що 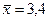, застосуємо формулу (12.6) заняття 12 для знаходження дисперсії

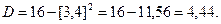
За формулою (12.5) заняття 12 знайдемо середнє квадратичне відхилення

.

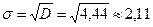Тоді за формулою (13.1) знайдемо коефіцієнт варіації

.

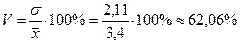Розділ 13.2. Медіана варіаційного ряду

Означення: Медіаною варіаційного ряду називається варіанта, яка припадає на середину варіаційного ряду.

Для дискретного розподілу медіана знаходиться досить просто. Можуть мати місце два випадки.

1). Обсяг сукупності є непарним числом :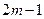

.

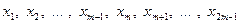Медіаною цього розподілу є варіанта 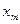, тому що до неї і після неї знаходиться по 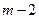варіанти, тобто

.

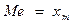2) Обсяг сукупності є парним числом, тоді за медіану приймають напівсуми варіант, що знаходяться в середині ряду

.

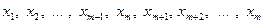Медіана цього розподілу є напівсумою варіант 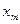і 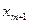, тому що до неї і після неї знаходиться по 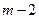варіанти, тобто

.

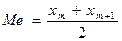Для неперервного розподілу, медіану можна обчислити за формулою

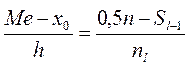, (13.2)

де 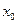- початкове значення медіанного інтервалу; 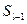- накопичена частота інтервалу, який знаходиться перед медіанним інтервалом; 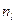- частота медіанного інтервалу; - довжина медіанного інтервалу (шаг); 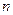- обсяг сукупності.

Приклад:

Дано розподіл 49 промислових підприємств за швидкістю обігових коштів. Знайти медіану даного розподілу.

Швидкість обігу, Кількість

в днях, підприємств

20 – 30 8

30 – 40 11

40 – 50 16

50 – 60 9

60 – 70 5

Всього: 49

Рішення

Знайдемо середину ряду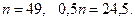

Розділимо вибірку на дві частини: меншу за 24,5 і більшу за 24,5.

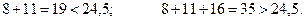
Значить медіанний інтервал (40 – 50). Тоді: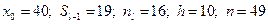

За формулою (13.2) обчислимо медіану

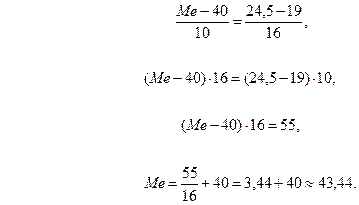
Поиск по сайту: