 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Розділ 14.3. Точність оцінки. Довірча ймовірність. Довірчий інтервал
 Точковою називається оцінка, що визначається одним числом. Інтервальною називається оцінка, що визначається двома числами – кінцями інтервалу. Інтервальні оцінки дозволяють встановити точність і надійність оцінок.
Точковою називається оцінка, що визначається одним числом. Інтервальною називається оцінка, що визначається двома числами – кінцями інтервалу. Інтервальні оцінки дозволяють встановити точність і надійність оцінок.
Означення: Надійністю (довірчою ймовірністю) параметра 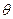 за статистичною оцінкою
за статистичною оцінкою  називається ймовірність
називається ймовірність 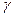 , з якою виконується нерівність
, з якою виконується нерівність  , де
, де  - додатнє число, що характеризує точність оцінки
- додатнє число, що характеризує точність оцінки
 .
.
Звичайно надійність оцінки 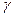 задається наперед числом, близьким до одиниці. Після елементарних перетворень одержуємо
задається наперед числом, близьким до одиниці. Після елементарних перетворень одержуємо
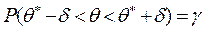 .
.
Це співвідношення свідчить, що ймовірність того, що інтервал  включає в себе (покриває) невідомий параметр
включає в себе (покриває) невідомий параметр 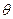 , дорівнює
, дорівнює 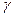 . А сам інтервал
. А сам інтервал  називається довірчим.
називається довірчим.
 Довірчий інтервал для оцінки математичного сподівання
Довірчий інтервал для оцінки математичного сподівання
нормального розподілу
Нехай кількісна ознака Х генеральної сукупності розподілена нормально, причому середнє квадратичне відхилення генеральної сукупності не відоме. Необхідно оцінити невідоме математичне сподівання 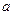 за допомогою довірчих інтервалів. За даними вибірки можна побудувати випадкову величину, яка має розподіл Ст’юдента з
за допомогою довірчих інтервалів. За даними вибірки можна побудувати випадкову величину, яка має розподіл Ст’юдента з  степенями свободи
степенями свободи
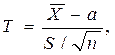
де  - вибіркова середня;
- вибіркова середня;  - виправлене середнє квадратичне відхилення;
- виправлене середнє квадратичне відхилення; 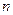 - обсяг вибірки.
- обсяг вибірки.
Щільність розподілу Ст’юдента має вигляд
 , де
, де 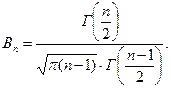
Ми бачимо, що розподіл Ст’юдента визначається параметром п – обсягом вибірки, що теж саме, що й числом степеней свободи  і не залежить від параметрів
і не залежить від параметрів 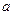 і
і 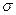 .
.
Знайдемо надійність параметра 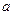
 .
.
Шляхом елементарних перетворень, перейдемо до подвійної нерівності
 .
.
Користуючись розподілом Ст’юдента, знайдемо довірчий інтервал, що покриває невідомий параметр 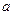 з надійністю
з надійністю 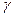
 . (14.8)
. (14.8)
За таблицею критичних точок розподілу Ст’юдента за заданими  і
і 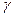 , можна знайти
, можна знайти  .
.
 Приклад:
Приклад:
Кількісна ознака Х генеральної сукупності розподілена нормально. За вибіркою обсягу  знайдено середню вибіркову
знайдено середню вибіркову  і виправлене середнє квадратичне відхилення
і виправлене середнє квадратичне відхилення  Оцінити невідоме математичне сподівання за допомогою довірчого інтервалу з надійністю
Оцінити невідоме математичне сподівання за допомогою довірчого інтервалу з надійністю 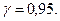
Рішення
За таблицею критичних точок розподілу Ст’юдента на перетині числа степеней свободи  і
і  (двостороння критична область), можна знайти
(двостороння критична область), можна знайти 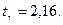
Тоді, за формулою (14.8) маємо

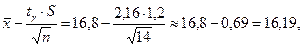
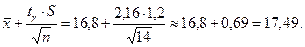
Таким чином, з надійністю 0,95 невідомий параметр 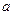 покриває довірчий інтервал
покриває довірчий інтервал 
 Довірчий інтервал для оцінки середнього квадратичного відхилення
Довірчий інтервал для оцінки середнього квадратичного відхилення
нормального розподілу
Нехай кількісна ознака Х генеральної сукупності розподілена нормально. Необхідно оцінити невідоме генеральне середнє квадратичне відхилення 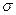 за виправленим середнім квадратичним відхиленням
за виправленим середнім квадратичним відхиленням  , тобто знайти довірчий інтервал, що покриває параметр
, тобто знайти довірчий інтервал, що покриває параметр 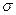 з заданою надійністю
з заданою надійністю 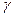 . Для цього необхідне виконання співвідношення
. Для цього необхідне виконання співвідношення

або
 .
.
Винесемо  за дужки і зробимо заміну
за дужки і зробимо заміну  , після чого одержимо
, після чого одержимо
 .
.
Тоді довірчий інтервал можна виразити за формулою
 . (14.9)
. (14.9)
На практиці, для знаходження  користуються таблицею значень, що наведена нижче. Але формула (14.9) справедлива при
користуються таблицею значень, що наведена нижче. Але формула (14.9) справедлива при  .
.
Таблиця значень 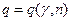
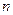
| 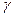
| 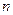
| 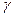
| ||||
| 0,95 | 0,99 | 0,999 | 0,95 | 0,99 | 0,999 | ||
| 1,37 | 2,67 | 5,64 | 0,37 | 0,58 | 0,88 | ||
| 1,09 | 2,01 | 3,88 | 0,32 | 0,49 | 0,73 | ||
| 0,92 | 1,62 | 2,98 | 0.28 | 0.43 | 0,63 | ||
| 0,80 | 1,38 | 2,42 | 0,26 | 0,38 | 0,56 | ||
| 0,71 | 1,20 | 2,06 | 0.24 | 0,35 | 0,50 | ||
| 0,65 | 1,08 | 1,80 | 0,22 | 0,32 | 0,46 | ||
| 0,59 | 0,98 | 1,60 | 0,21 | 0,30 | 0,43 | ||
| 0,55 | 0,90 | 1,45 | 0,188 | 0,269 | 0,38 | ||
| 0,52 | 0,83 | 1,33 | 0,174 | 0,245 | 0.34 | ||
| 0,48 | 0,78 | 1,23 | 0,161 | 0.226 | 0,31 | ||
| 0,46 | 0,73 | 1,15 | 0,151 | 0,211 | 0,29 | ||
| 0,44 | 0,70 | 1,07 | 0,143 | 0,198 | 0,27 | ||
| 0,42 | 0,66 | 1,01 | 0,115 | 0,160 | 0,211 | ||
| 0,40 | 0,63 | 0,96 | 0,099 | 0,136 | 0,185 | ||
| 0.39 | 0,60 | 0,92 | 0,089 | 0,120 | 0,162 |
Якщо  , тоді нерівність (14.9) набуде вигляду (враховуємо, що
, тоді нерівність (14.9) набуде вигляду (враховуємо, що 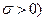
 . (14.10)
. (14.10)
 Приклад:
Приклад:
Кількісна ознака Х генеральної сукупності розподілена нормально. За вибіркою обсягу  знайдено виправлене середнє квадратичне відхилення
знайдено виправлене середнє квадратичне відхилення  . Знайти довірчий інтервал, що покриває генеральне середнє квадратичне відхилення
. Знайти довірчий інтервал, що покриває генеральне середнє квадратичне відхилення 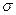 з надійністю 0,95.
з надійністю 0,95.
Рішення
За таблицею значень  за даними
за даними 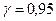 і
і  знайдемо
знайдемо  Тоді за формулою (14.9)
Тоді за формулою (14.9)
 ,
,
 .
.
Таким чином, довірчий інтервал  покриває невідомий параметр генеральної сукупності
покриває невідомий параметр генеральної сукупності 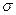 з надійністю 0,95.
з надійністю 0,95.
 Приклад:
Приклад:
Кількісна ознака Х генеральної сукупності розподілена нормально. За вибіркою обсягу  знайдено виправлене середнє квадратичне відхилення
знайдено виправлене середнє квадратичне відхилення  . Знайти довірчий інтервал, що покриває генеральне середнє квадратичне відхилення
. Знайти довірчий інтервал, що покриває генеральне середнє квадратичне відхилення 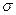 з надійністю 0,99.
з надійністю 0,99.
Рішення
За таблицею значень  за даними
за даними 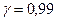 і
і  знайдемо
знайдемо  Тоді за формулою (14.10)
Тоді за формулою (14.10)
 ,
,
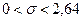 .
.
Таким чином, довірчий інтервал  покриває невідомий параметр генеральної сукупності
покриває невідомий параметр генеральної сукупності 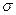 з надійністю 0,99.
з надійністю 0,99.
Поиск по сайту: