АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Розділ 13.3. Мода варіаційного ряду

Читайте также:
  1. Висновки до 3 розділу
  2. ВІДЦЕНТРОВІ ПИЛЕОСАДНІІ СУСПЕНЗІЙНО- РОЗДІЛЬНІ АПАРАТИ (ЦИКЛОНИ)
  3. Вставка розриву сторінки або розділу
  4. Демультиплексор (роздільник) Demux
  5. Для військових психологів щодо підготовки особового складу підрозділів і частин до участі в бою і проведення психологічної реабілітації військовослужбовців із БПТ
  6. Додаткова література до розділу І
  7. ЗАВДАННЯ ДЛЯ ПЕРЕВІРКИ І САМОПЕРЕВІРКИ ЗАСВОЄННЯ РОЗДІЛУ «ДИДАКТИКА»
  8. ЗАВДАННЯ ДЛЯ САМОКОНТРОЛЮ ТА САМОСТІЙНОЇ РОБОТИ СТУДЕНТІВ ЗА РОЗДІЛОМ ХІ.
  9. ЗАВДАННЯ ДЛЯ САМОКОНТРОЛЮ ТА САМОСТІЙНОЇ РОБОТИ СТУДЕНТІВ ЗА РОЗДІЛОМ ХІІ.
  10. ЗАВДАННЯ ДЛЯ САМОКОНТРОЛЮ ТА САМОСТІЙНОЇ РОБОТИ СТУДЕНТІВ ЗА РОЗДІЛОМ ХІІІ.
  11. ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ І ЗАПИТАННЯ ДЛЯ САМОКОНТРОЛЮ ЗА РОЗДІЛОМ І.
  12. ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ І ЗАПИТАННЯ ДЛЯ САМОКОНТРОЛЮ ЗА РОЗДІЛОМ ІІ.

Означення: Модою варіаційного ряду називається варіанта, що найбільш часто зустрічається, тобто має найбільшу частоту.

Як видно з означення, при дискретному розподілі знаходження значення моди не потребує будь-яких складних обчислень. Із статистичного розподілу обирається найбільша частота і варіанта, яка їй відповідає і є модою.

Для неперервного розподілу мода обчислюється за формулою

 

 

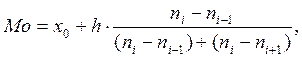(13.3)

 

де 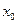- початкове значення модального інтервалу; - довжина модального інтервалу (шаг); - частота модального інтервалу; - частота інтервалу, який знаходиться перед модальним; - частота інтервалу, який знаходиться після модального.

 

 

Приклад:

Для попереднього прикладу про розподіл 49 промислових підприємств за швидкістю обігових коштів, знайти моду даного розподілу.

 

Рішення

 

За формулою (13.3) обчислимо моду статистичного ряду. Оскільки , то інтервал (40 – 50) є модальним.

 

 

 

Ляпунов Олександр Михайлович (6.06.1857 – 3.11.1918 рр.) – російський математик і механік, професор, академік. Зробив важливий внесок до теорії ймовірностей, дав просте і строге доведення центральної граничної теореми у більш загальній формі, для цього розробив оригінальний метод характеристичних функцій, який широко застосовується у сучасній теорії ймовірностей.

Розділ 13.4. Асиметрія і ексцес

Для введення таких числових характеристик, як асиметрія і ексцес, необхідно спочатку ввести поняття моментів варіаційного ряду.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)