Розділ 7.3. Завдання до заняття 7

1. Сформулювати теорему про математичне сподівання відхилення випадкової величини.

2. Дати означення дисперсії.

3. Сформулювати теорему, що полегшує обчислення дисперсії.

4. Перелічити властивості дисперсії.

5. Дати означення середнього квадратичного відхилення.

Розділ 8.1. Функція розподілу (інтегральна функція) та її властивості

Як відомо із заняття 6 неперервною випадковою величиною називають таку величину, яка може приймати всі значення з деякого скінченного або нескінченного проміжку, тому задати її закон розподілу за допомогою таблиці неможливо.

Таким чином для описання неперервної випадкової величини необхідно припустити, що відома ймовірність попадання Х у довільний інтервал або відома функція розподілу ймовірностей.

Означення: Функцією розподілу (інтегральною функцією розподілу) випадкової величини Х називається ймовірність того, що випадкова величина Х прийме значення менше від фіксованого дійсного числа х, тобто

. (8.1)

Геометрична інтерпретація функції розподілу полягає у наступному. Якщо випадкову величину розглядати як випадкову точку на осі Ох (рис. 1), яка за результатом випробування може зайняти те чи інше положення на цій осі, то функція є ймовірність того, що випадкова точка Х у результаті випробування попадає лівіше х.

Рис.1. Геометрична інтерпретація всіх можливих значень функції розподілу.

Неперервна випадкова величина має неперервну функцію розподілу, графік якої має форму плавної кривої (рис. 2).

Рис.2. Геометрична інтерпретація функції розподілу неперервної випадкової величини.

Розглянемо загальні властивості функції розподілу.

Властивість 1: Функція розподілу F(x) є невід’ємною величиною, яка міститься між нулем і одиницею

.

Дійсно, це випливає з означення інтегральної функції як ймовірності і властивості ймовірності.

Властивість 2: Функція розподілу F(x) є неспадною функцією, тобто , якщо .

Доведення

Нехай . Подія, яка полягає в тому, що випадкова величина Х приймає значення менше за , складається з двох подій:

1) або Х прийме значення менше х₁ і ;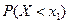

2) або Х прийме значення з проміжку і .

Тоді за теоремою додавання ймовірностей маємо

,

або

. (8.2)

Із формули (8.2) випливає

, бо .

Наслідок 1: Ймовірність того, що випадкова величина прийме значення із проміжку , дорівнює приросту функції на цьому проміжку, тобто

. (8.3)

Приклад:

Випадкова величина задана інтегральною функцією

Знайти ймовірність того, що випадкова величина Х прийме значення з проміжку [-2,0).

Рішення

За формулою (8.3) маємо

,

тобто

Наслідок 2: Ймовірність того, що неперервна випадкова величина Х прийме певне значення дорівнює нулю.

Доведення

Підставимо у формулу (8.3) 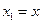, , тоді

.

Нехай . Оскільки Х - неперервна випадкова величина, то функція теж неперервна, внаслідок цього маємо, що приріст в точці , тобто , а значить

. (8.4)

Підкреслимо, що формула (8.4) теж тільки для неперервних випадкових величин, на відміну від дискретних.

Враховуючи формулу (8.4), можна записати

.

Наприклад:

.

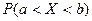Властивість 3: На мінус нескінченності функція розподілу дорівнює нулю, а на плюс нескінченності функція розподілу дорівнює одиниці, тобто

; .