Методика обчислення теоретичних частот нормального розподілу

Розглянемо один із способів обчислення теоретичних частот в припущенні, що генеральна сукупність розподілена нормально.

1. Весь інтервал спостережувальних значень Х вибірки обсягу 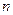ділять на 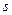частинних інтервалів . Знаходять середини частинних інтервалів 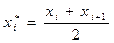. Одержуємо варіаційний ряд

			...
			...

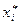
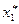
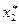
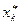
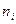
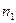
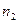
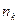
2. Обчислюємо вибіркову середню 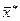і вибіркове середнє квадратичне відхилення .

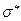3. Нормуємо випадкову величину Х, тобто переходимо до величини 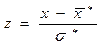і обчислюємо кінці інтервалів

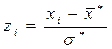і 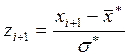. (15.7)

При цьому найменше значення 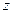, тобто 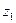, беруть рівним 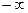, а найбільше 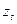беруть рівним .

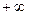4. Обчислюємо теоретичні ймовірності 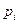попадання Х в інтервал за формулою

, (15.8)

де 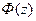- функція Лапласа.

5. Обчислюємо шукані теоретичні частоти за формулою

. (15.9)

Приклад:

Обчислити теоретичні частоти за заданим інтервальним розподілом вибірки обсягу 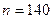, припускаючи, що генеральна сукупність розподілена нормально.

№ п/п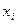

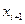
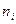
Рішення

Результати розрахунків занесемо до таблиц 1

Таблиця 1

№ п/п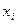
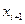
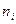
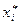
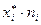
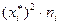
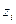
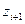
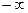
								-1,05
							-1,05	-0,16
							-0,16	0,44
							0,44	1,03
							1,03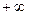

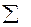
Знайдемо середню вибіркову: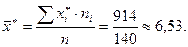

Знайдемо вибіркове середнє квадратичне відхилення: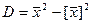

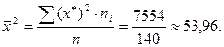
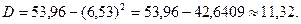
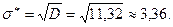
Нормуємо випадкову величину Х за формулами (15.7), результати обчислень запишемо у 8 і 9 стовпці таблиці 2.

Таблиця 2

№ п/п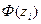
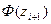
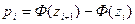
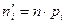
	- 0,5	- 0,3531	0,1469	20,566
	- 0,3531	- 0,0636	0,2895	40,53
	- 0,0636	0,1700	0,2336	32,704
	0,1700	0,3485	0,1785	24,99
	0,3485	0,5	0,1515	21,21

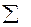
За таблицею функції Лапласа знаходимо значення 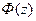, при цьому враховуємо, що 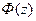є непарною функцією, тобто 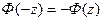і для значень 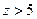, 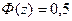(стовпці 2 і 3 продовження таблиці).

Обчислюємо теоретичні ймовірності 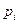за формулою (15.8) (стовпчик 4 продовження таблиці): .

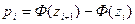Обчислюємо шукані теоретичні частоти за формулою (15.9) (стовпчик 5 продовження таблиці): .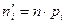

Як бачимо,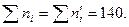

Поиск по сайту: